Mimari, inşaat ve tasarımda altın oran kuralı

Doğanın gözlemleri ve güzel yaratıklarının sırlarını ortaya çıkarmaya yönelik girişimler pek çok keşif getirdi. Bunlardan biri altın oran. Bu, güzel dediğimiz her şeye uyan belli bir kalıptır. İnsanlar, hayvanlar, çiçekler, binalar, galaksiler ...

Altın oran nedir ve nasıl anlaşılır

Genellikle bizi bir şeylerle büyüleyen evler, nesneler, binalar, bitkilerle karşılaşırız. İnsanlar uzun zamandır bir şeyin bize neden güzel göründüğünü, diğerinin olmadığını anlamaya çalıştılar, kalıp arıyorlardı. Ve onu bulmuş görünüyorlar. Bu, altın oran olarak adlandırılan belirli bir parça oranıdır.

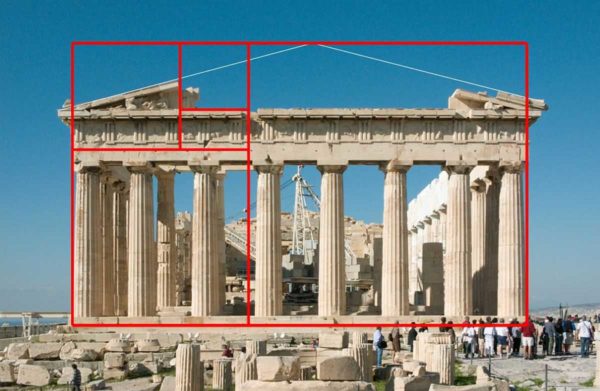
Altın oranı kimin ve ne zaman icat ettiği hakkında kimse kesin olarak bilmiyor. Birisi keşfi Pisagor'a atfediyor, ancak ilk söz Öklid'in "Öğeleri" nde bulundu ve MÖ 3. yüzyılda yaşadı. Yani keşif açıkça eski. Antik Yunan ve Roma tapınakları bu ilke üzerine inşa edilmiştir. Elbette bunlar tesadüf olabilir ama çok tuhaflar ve birçoğu var. Yani, büyük olasılıkla ideal oranların farkındaydılar.

Hayatta kalan antik binalar da altın bölümün kuralına tabidir.

Leonardo da Vinci'nin insan vücudunun yapısında bu prensibin onayını aradığı kesinlikle kesindir. Ve en ilginç olanı buldum. Bize güzel görünen bu yüzler ve bedenler, sadece altın oran kanununa uyan oranlara sahiptir.

Biçimsel tanım hem basit hem de karmaşık geliyor. Farklı boyutlarda iki segmentle ilişkilidir. Bu ilke şuna benzer bir şeye benziyor: eğer bir parça iki eşit olmayan parçaya bölünürse, o zaman bölümün çoğu bütünü ile aynı şekilde küçük parça büyük bölümle ilişkiliyse bu bölme orantılı olacaktır. Resme ve formüle bakarsanız daha net olacaktır.

Altın oranın ilkesi ve formülü

Şekilde, tüm segment bölünmüştür, böylece a bölünmek b1.1618 alıyoruz, tüm segment büyük bir bölüme bölünürse aynı rakam elde edilir - a... Bu sayı, ideal oranın somutlaşmış halidir. Şimdi, Parthenon'un resmine bakarsanız, bu yapının oranları da belirtilen orana uyuyor.

Aynı model yüzde olarak gösterilebilir. Belki birisi için daha kolaydır. Bütünün bölünmesinin orantılı olabilmesi için parçaların% 62 ve% 38 olması gerekir. Bu şekilde hatırlamak daha kolay olabilir.

Fibonacci dizisi sadece matematiksel bir formül değildir

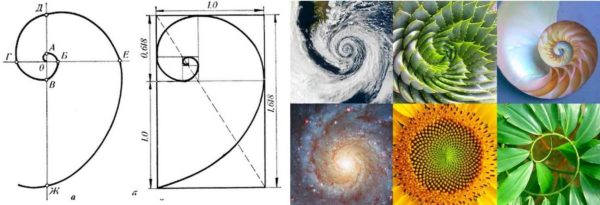
Bu model matematikçi Fibonacci tarafından daha da geliştirildi. Dokuzuncudan başlayarak aynı yasaya uyan sayısal bir dizi geliştirdi. Bu sekansın grafik temsili bir sarmaldır. Yakından bakarsanız doğada, mimaride ve insan vücudunda güzellik oranları vardır.

Mükemmel oranlara sahip bir dikdörtgen nasıl oluşturulur

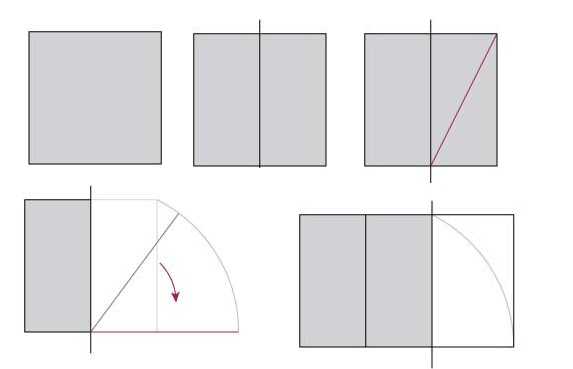
Pratikte alınan bilgileri uygulamak için, mekanı bir şekilde bölmeyi veya bu yasaya göre inşa etmeyi öğrenmesi gerekir. İlk önce, mükemmel oranlarda bir dikdörtgen oluşturmayı öğrenelim. Temel olarak bir kare alıyoruz.

Altın oranlı bir dikdörtgen oluşturur

Kareyi ikiye bölün, karşıt köşeleri birbirine bağlayan dikdörtgenlerden birine bir çizgi çizin. Sonra bir pusula alıyoruz, karenin alt tarafının ortasına bir iğne koyuyoruz, ortaya çıkan köşegenin uzunluğunu bir kenara bırakıp karenin alt tarafının devamı olacak bir çizgi üzerine işaretliyoruz.Elde edilen dikdörtgenin en boy oranı 1,62'dir (bu tam olarak% 62 ve% 38 veren orandır).

Bu açıkça tesadüf değil. Her şey bu kalıba uymasa da

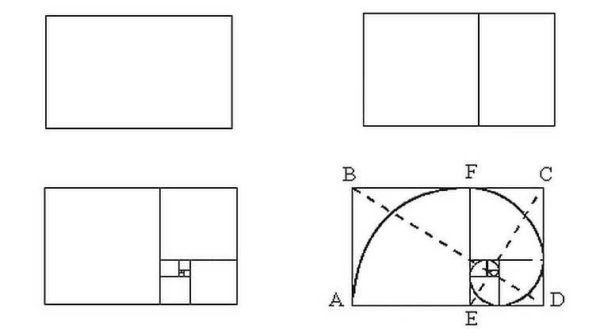
Daha da ilginci, 1.62 dikdörtgeni bir kare ve bir dikdörtgene bölmeye başlarsanız, yine mükemmel oranlara sahip ancak daha küçük bir dikdörtgen elde edeceksiniz. Aynı ilkeye göre tekrar bölerseniz, oranı altın orana karşılık gelecek olan kenarları olan başka bir kare + dikdörtgen çifti olacaktır. Ve böylelikle bölümü tamamlayana kadar devam edin. Ama daha da ilginç olanı, Fibonacci serisi, gevşeyen bir spiral gibi görünen bu bölüme mükemmel bir şekilde uyuyor. Yukarıdaki resimdeki şekle bakın.

Altın oran kuralına göre bir segment nasıl bölünür?

Bu beceri, örneğin bir ev projesi oluştururken, planlarken, bir apartman tasarımı geliştirirken, mobilya düzenlerken vb. Kullanışlı olacaktır. Ayrıca bir alan, çiçek tarhları, bitki dikimi vb. Planlanırken de gerekli olabilir. Genel olarak hemen hemen her yerde kullanılabilir.

Fantezi değil ama gözlerini alamazsın. Neden biliyor musun?

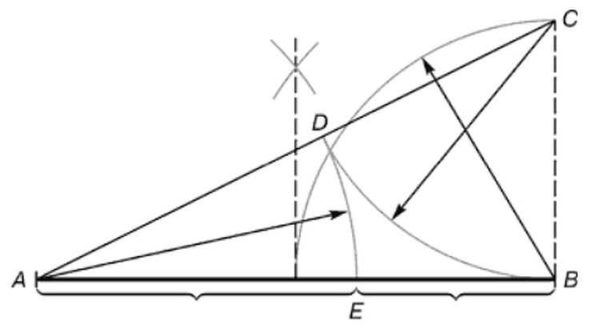
Öyleyse, bir bölümü altın bölüm kuralına göre bölme sırası:

• Bir segment alıyoruz, ikiye bölüyoruz.
• Uçlardan birinden, segmentin uzunluğunun yarısı olan dik (90 ° 'lik bir açıyla düz çizgi) geri yükleriz. Şekilde, bu bir segmenttir M.Ö.
• Alınan nokta C segmentin diğer ucuna düz bir çizgi bağlayın (Bir).
• Segmentte AC bir noktaya değinmek D... Segmentin uzunluğuna eşit bir mesafede bulunur M.Ö... Bunu yapmanın en kolay yolu pusuladır, ancak bir cetvel de kullanabilirsiniz.
• Segmentin uzunluğunu ölçüyoruz AD (yine bir pusula veya bir cetvelle). Segmentte aynı uzunluğu erteleriz AB... Noktayı anladık E.
• Şimdi, segmentlerin uzunluklarını ölçerseniz AE ve EB ve onları bölün, aynı imrenilen sayıyı elde ederiz - 1.62.

Bir segmenti ideal bir oranla bölümlere ayırmak

Prosedürü birkaç kez tekrarlayarak, her şeyi tam anlamıyla birkaç dakika içinde nasıl yapacağınızı öğreneceksiniz. Örneğin, pencerenin yüksekliğini, şeklini belirlemek için ihtiyacınız varsa, bu oranları da kullanabilirsiniz. Aynı prensip ile tüm mimari elemanların yerini, boyutlarını belirlemek mümkündür. Mevcut nesneleri planlarken, yüzde kullanarak bölmek daha kolaydır. Burada ya kafanızda sayarsınız ya da bir hesap makinesi kullanırsınız.

Mükemmel üçgen ve pentagram

Bir ikizkenar üçgen ideal olarak adlandırılır ve tabanı yan uzunluğa 1/3 olarak atıfta bulunur. Yani yine altın oran gözlenir. İdeal en boy oranına sahip bir üçgen çizmek zor değil. Pusula ile daha kullanışlıdır, ancak bir cetvelle geçebilirsiniz.

Altın üçgen, örneğin bir iç mekanın yaratılmasında yapımının ve uygulamasının kuralı

İnşaat aşağıdaki gibidir. Bir noktadan düz bir çizgide Bir keyfi uzunlukta bir segmenti üç kez bir kenara koyun. Bu uzunluğu gösteriyoruz Ö... Noktayı anladık B... Parçaya dik olarak içinden düz bir çizgi çizin AB... Bu çizgide noktanın her iki tarafına B değeri bir kenara koymak Ö... İki puan alıyoruz d ve d1... Onları bir nokta ile birleştiriyoruz Bir... Böylece kenarları 1.62 ile ilişkili olan bir üçgenimiz var. Tabanın uzunluğunu yan taraftaki bir pusula ile ertelerseniz bunu kontrol edebilirsiniz (nokta C). İkinci kontrol, zıt açının 36 ° olmasıdır.

Bir pentagram inşa etmek biraz daha karmaşıktır. Onu bir daireye yazıyoruz, pusula olmadan yapamayız.

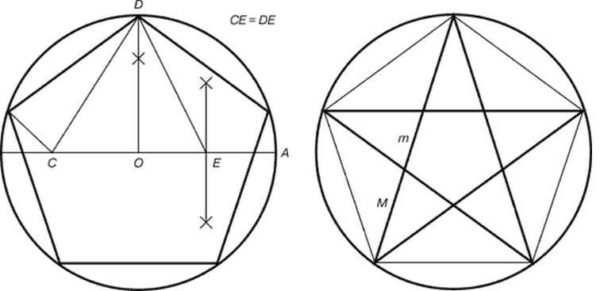
• Çemberin merkezi şu şekilde gösterilir: Ö, daire ile kesişene kadar içinden düz bir çizgi çizin. Kesişme noktalarından biri gösterilir Bir... Çizgi segmenti OA Çemberin çapıdır.
• Segmentin ortasını bulun OD, bir noktaya değin E... Dik olanı çemberin merkezinden çemberle kesişme noktasına kadar geri yükleyin. Nokta bu D.

Pentagram inşa etmek

• Noktaları birleştir E ve D... Bir pusula yardımıyla, yarıçapta bir noktayı erteliyoruz C... Çizgi segmenti CD segmentin uzunluğuna eşit ED... Segmentin uzunluğunu bir pusula ile ölçüyoruzED... İğneyi noktaya koyuyoruz E, ucu yarıçapla kesişme noktasına götür. Böylece noktayı anladık C.
• Segmentin uzunluğu DC - pentagramın kenarı. Ölçüyoruz, pusula yardımıyla bir daireye aktarıyoruz. Bunu yapmak için, gecikmiş mesafeli bir pusula ile, daireye dört nokta daha koyarız, bunları sırayla birleştiririz, bir pentagram alırız.

İşte ilginç olan şey, ortaya çıkan pentagramın köşeleri bir yıldız çizmek için kullanılırsa, mükemmel üçgenlerden oluşacaktır.

İnşaatta uygulama

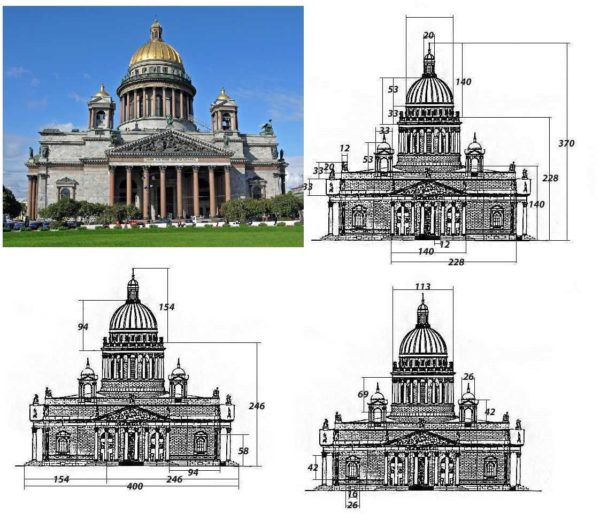
Daha önce de belirtildiği gibi altın oranı kimin keşfettiği bilinmiyor ama bize güzel görünen her şey tam olarak bu en boy oranına sahip. Doğada pek çok örnek var. Tanınmış binaları ele alırsak, aynı model de var.

Isaac Katedrali - eğlenmek için sayabilirsiniz

Evinizin içten dışa çekici, hatırlanmasını ve beğenilmesini istiyorsanız, bir proje oluştururken veya seçerken en azından temel oranlar hesaplanabilir. Orantılı ayarlamalar yapmak her zaman kolay olmayabilir ve genellikle ek maliyetler içerir. Ancak, bir proje oluştururken altın oranı göz önünde bulundurursanız, sorular kendiliğinden kaybolur. Aslında o kadar da zor değil.

Örneğin, yaklaşık 100 metrekarelik bir ev istediğinizi varsayalım. Uzun kenar 12 metreye kadar alınabilmektedir. Daha sonra kısa olan uzun olanın% 62'sidir ve 7.44 metre olacaktır. 7 metre veya 7,5 metre yapabilir, 8'e çıkarabilirsiniz. Kesin, bir santimetreye kadar ölçülere uyum hiç gerekli değildir. Oran önemlidir. Ve "gözle" yaklaşımda bile uyumlu görünüyor. Bu durumda inşaat alanı biraz daha küçüktür - 90-96 kare. Daha fazlasına ihtiyacınız varsa, 13 metreye eşit uzun kenarı alın ve tekrar sayın. Bir ev planı oluştururken altın oranın nasıl kullanılacağı anlaşılabilir gibi görünüyor.

Binanın ana parametreleri doğru orandaysa, bina her tarzda ilginç görünüyor.

Bu durumda kat yüksekliği, en uzun kısmın% 32'si olarak alınır. 12 * 0.32 = 3.84 metre olacaktır. Prensip olarak bu, odanın konforlu boyutları hakkındaki mevcut fikirlere karşılık gelir, ancak dilerseniz yüksekliği küçültebilirsiniz. Evin diğer tüm parçaları da yaklaşık olarak hesaplanır.

Evin de manzaraya uyması gerektiğini unutmayın. Bir tür baskın varsa - örneğin yüksek bir tepe, o zaman tepe ile oran ve arsa oranları hesaplanmalıdır. Genel olarak, uyumlu bir mülk oluşturmak için birçok faktör dikkate alınmalıdır.

Yalnızca düz çizgiler kullanılamaz. Doğru, kavisli yüzeylerle çalışmak daha zordur ve daha pahalıdır - standart olmayan bir cihaz her zaman daha pahalıdır

Aynı ilkeye göre, mümkünse gerekli orana uymaya çalışan bir iç düzen geliştirirler. Ama bir kez daha tekrarlayacağız: mümkünse. Santimetre ile tam olarak yazışmaya takılmayın. Genel eğilim önemlidir.

İç tasarımda altın oran

Altın Oran görsel zevkin yanı sıra başka ne sağlar? Psikologlar, bu kurala göre oluşturulan bir iç mekanda kişinin daha rahat hissettiğini söylüyor. Bu elbette özneldir, ancak deneyebilirsiniz. Öyleyse, iç tasarımda altın oran şöyle yorumlanıyor:

• Odayı bölgelere ayıracaksanız, kuralı kullanın. Bu, parçalardan birinin yaklaşık% 62, diğerinin -% 38 olması gerektiği anlamına gelir.
• Mobilya parçalarının kapladığı alan 2 / 3'ten fazla olmamalıdır.
• Mobilya seçerken, kurala göre hareket ediyoruz: boyutlar açısından her bir orta öğe, büyük ve küçük ila orta anlamına gelir.
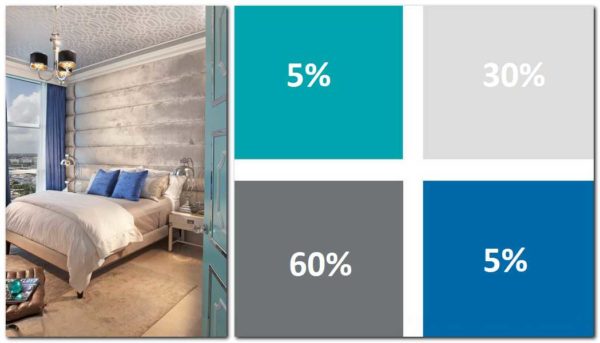
• Bir renk seçerken, aşağı yukarı aynı kuralları izleyin:
  • Ana renk yaklaşık 2/3, tüm ek ve vurgu renkler 1 / 3'tür. Renkler, belirli kurallara göre eşleşecek şekilde seçilir.
  • İkinci seçenek:% 60 ana renk,% 30 ek ve% 10 vurgu.
    

    Doğru orantılılık kurallarına göre renk eşleştirme örneği

• Yatay bölme duvar (panel) kullanılırken, panel yüksekliği oda toplam yüksekliğinin 1 / 3'ü veya 2 / 3'ü olarak alınabilir. Ancak aynı zamanda, mobilya uzunluk olarak değil orantılı olarak seçilir.

Mobilya ile ilgili olarak, kural anlaşılmaz görünüyor, ancak bu sadece ilk bakışta. Örneğin, bir rekreasyon grubu seçiyoruz. Bu durumda büyük bir nesne bir kanepe veya kanepedir. Orta - kahve veya sehpa, koltuklar. Küçük olanlar - aksesuarlar. Bu nedenle sehpanın boyutları, kanepenin uzun kenarından, koltuktan - kısa kenarından fazla olmamalıdır. Aksesuarlar bir masa veya sandalyeden daha büyük değildir. İdeal olarak, onlarla% 62 ve% 38 olarak ilişkilidirler.

Orantılılık önemli bir şeydir

Kesin oran neden belirtilmiyor? Çünkü öncelikle bu tür eşyaları bulmak gerçekçi değildir. İkinci olarak altın oran sadece% 62 ve% 38 değildir. Aynı zamanda, tasarımı uyumlu hale getiren Fibonacci dizisidir. Bu diziyi "yerleşik işlev" olarak gören insanlar var. Saymalarına gerek yoktur, yetenek ve sezgiye göre seçim yaparlar. Ancak seçimlerini analiz ederseniz, oranlar ideale yakın olacaktır. Bunun gibi.

Altın oran peyzaj tasarımı

Bir sitede bir manzara oluştururken, ideal oranlar ilkesi uygulanır ve buna üçgen kuralı denir. Kompozisyonun bir baskın olması gerekir, bileşenlerinin geri kalanı sadece vurgular, onu ortaya çıkarır. Örneğin, arsada büyük bir ağaç var ve onu yenmek istiyorsunuz. Kompozisyonun merkezi olacak - baskın. Bir plana koy, hizala çiçeklik veya taş döşeli bahçe, kaya bahçesi - ne yapmak istiyorsun.

Bahçe tasarımında üçgen kuralı

Baskın bitki veya taştan dik açılarla iki çizgi çizin. Bu hatlara alt bitkilerin dikilmesi gerekecektir. Ayrıca, ikinci en yüksek, ana nesnenin yüksekliğinin 2 / 3'ünden daha yüksek olmamalıdır. Üçüncü nesne 1 / 3'ten yüksek değildir. Kompozisyonu daha da bodur dikimlerle tamamlarlar. Bu, altın oranın dikim planlamasına nasıl uygulanacağına dair hızlı bir rehberdir.

Ama hepsi bu kadar değil. Bitkiler renge göre seçilmelidir - farklı tonlardaki yeşillikler, çiçek lekeleri ve dekoratif yaprak döken bitkilerin bir kombinasyonu - her şey aynı yasaya uyar. Baskın gölge yaklaşık% 60, tamamlayıcı renkler -% 30, vurgular -% 10'dur. Bu, bir gruptaki seçim kuralları hakkında konuşursak olur. Ama aynı zamanda tüm planı bir bütün olarak - boyut, yükseklik, renkler - koordine etmeniz gerekir.