The golden ratio rule in architecture, construction and design

Observations of nature and attempts to uncover the secrets of her beautiful creatures have brought a lot of discovery. One of them is the golden ratio. This is a certain pattern that obeys everything that we call beautiful. People, animals, flowers, buildings, galaxies ...

What is the golden ratio and how to understand it

Often we come across houses, objects, buildings, plants that fascinate us with something. People have long tried to understand why one thing seems beautiful to us, the other is not, they were looking for patterns. And they seem to have found it. This is a certain ratio of parts, which was called the golden ratio.

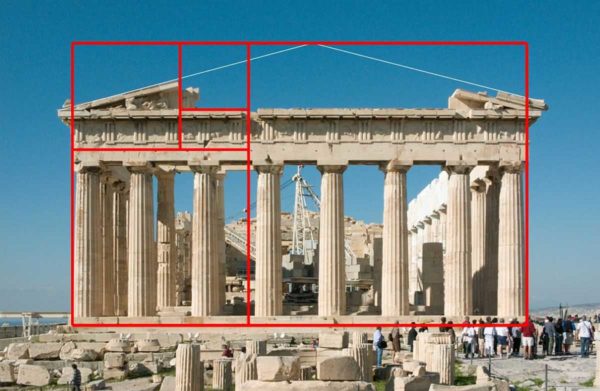
About who and when invented the golden ratio, no one knows for sure. Someone attributes the discovery to Pythagoras, but the first mention was found in the "Elements" of Euclid, and he lived in the 3rd century BC. So the find is clearly old. It is on this principle that ancient Greek and Roman temples were built. Of course, these may be coincidences, but they are very strange and there are a lot of them. So, most likely, they were aware of the ideal proportions.

The surviving buildings of antiquity are also subject to the rule of the golden section

It is absolutely certain that Leonardo da Vinci was looking for confirmation of this principle in the structure of the human body. And, what is most interesting, I found it. Those faces and bodies that seem beautiful to us have proportions that just obey the law of the golden ratio.

The formal definition sounds both simple and complex. It is associated with two segments of different sizes. This principle sounds something like this: if a segment is divided into two unequal parts, then this division will be proportional if most of the segment refers to the whole in the same way as the smaller part to the larger. It will be clearer if you look at the illustration and the formula.

Principle and formula of the golden ratio

In the figure, the whole segment is divided so that if a split into b, we get 1.1618, the same figure is obtained if the whole segment is divided by a large part - a... This number is the embodiment of the ideal proportion. Now, if you look at the picture of the Parthenon, the proportions of this structure also obey the indicated ratio.

The same pattern can be represented as percentages. Maybe it's easier for someone. In order for the division of the whole to be proportional, the parts must be 62% and 38%. It might be easier to remember this way.

The Fibonacci sequence is not just a mathematical formula

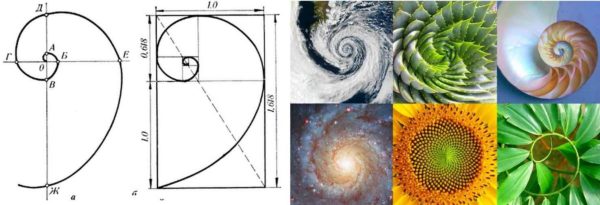
This pattern was developed further by the mathematician Fibonacci. He developed a numerical sequence, the elements of which, starting from the ninth, obey the same law. The graphic representation of this sequence is a spiral. If you look closely, there are proportions of beauty in nature, in architecture, and in the human body.

How to build a rectangle with perfect proportions

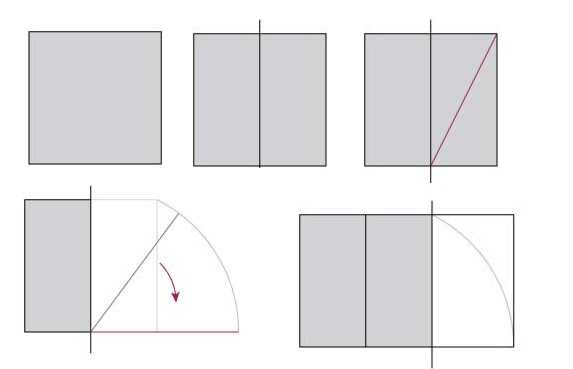
In order to apply the information received in practice, one must somehow learn to divide the space or build it according to this law. First, let's learn how to build a rectangle with perfect proportions. We take a square as a basis.

Creates a rectangle with a golden ratio

Divide the square in half, draw a line in one of the resulting rectangles that connects the opposite corners. Then we take a compass, put the needle in the center of the lower side of the square, set aside the length of the resulting diagonal and mark it on a line that will be a continuation of the lower side of the square.The resulting rectangle has an aspect ratio of 1.62 (this is exactly the ratio that gives 62% and 38%).

This is clearly no accident. Although not everything obeys this pattern

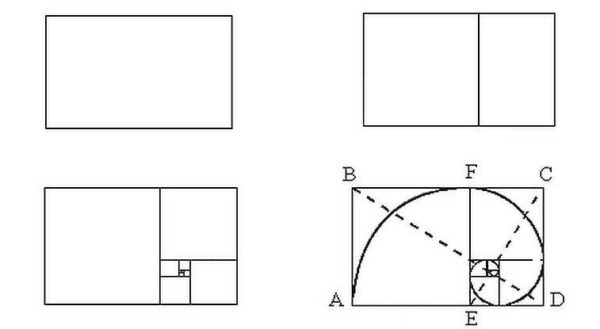
What's more interesting is that if you start dividing the 1.62 rectangle into a square and a rectangle, you will again get a rectangle with perfect proportions, but smaller. If you divide it again according to the same principle, there will be another pair of square + rectangle with sides, the ratio of which will correspond to the golden ratio. And so on until you can carry out the division. But what is even more interesting, the Fibonacci series fits perfectly into this division, which looks like an unwinding spiral. See illustration in the picture above.

How to divide a segment according to the rule of the golden ratio

This skill will come in handy, for example, when creating a house project, planning, when developing an apartment design, arranging furniture, etc. It may also be needed when planning a site, flower beds, planting plants, etc. In general, it can be used almost everywhere.

Nothing fancy, but you can't take your eyes off. Do you know why?

So, the order of dividing a segment according to the rule of the golden section:

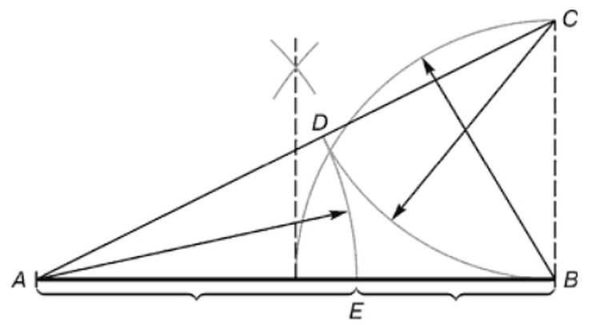
• We take a segment, divide it in half.
• From one of the ends we restore a perpendicular (straight line at an angle of 90 °), which is half the length of the segment. In the figure, this is a segment BC.
• Received point C connect a straight line with the other end of the segment (A).
• On the segment AC put a point D... It is located at a distance equal to the length of the segment BC... The easiest way to do this is with a compass, but you can also use a ruler.
• We measure the length of the segment AD (again with a compass, or a ruler). We postpone the same length on the segment AB... We get the point E.
• Now, if you measure the lengths of the segments AE and EB and divide them, we get the same coveted number - 1.62.

Dividing a segment into sections with an ideal ratio

Repeating the procedure a couple of times, you will learn how to do everything in literally a matter of minutes. If you need, for example, to determine the height of the window, its shape, you can also use these proportions. By the same principle, it is possible to determine the location of all architectural elements, their sizes. When planning existing objects, it is easier to divide by using a percentage. Here you either count in your head, or use a calculator.

Perfect triangle and pentagram

An isosceles triangle is called ideal, the base of which refers to the side length as 1/3. That is, again the golden ratio is observed. It's easy to draw a triangle with the perfect aspect ratio. It is more convenient with a compass, but you can get by with a ruler.

The golden triangle, the rule of its construction and application in the creation of an interior, for example

The construction is as follows. On a straight line from a point A postpone a segment of arbitrary length three times. We denote this length O... We get the point B... Draw a straight line through it, perpendicular to the segment AB... On this line to both sides of the point B set aside the value O... We get two points d and d1... We connect them with a dot A... So we got a triangle, the sides of which are related as 1.62. You can check this if you postpone the length of the base on the lateral side with a compass (point C). The second check is that the opposite angle is 36 °.

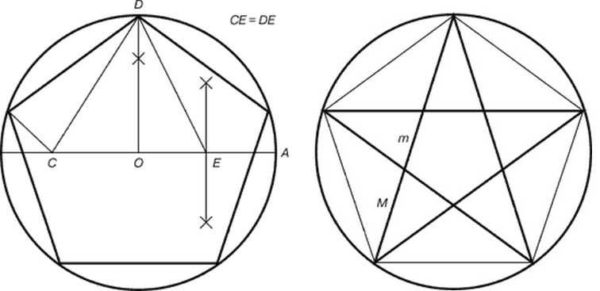
Building a pentagram is a little more complicated. We inscribe it in a circle, we cannot do without a compass.

• The center of the circle is denoted by O, draw a straight line through it until it intersects with the circle. One of the intersection points is denoted A... Line segment OA Is the diameter of the circle.
• Find the middle of the segment OD, put a point E... Restore the perpendicular from the center of the circle up to the intersection with the circle. This is the point D.

Building a pentagram

• Connect the dots E and D... With the help of a compass, we put off a point on the radius C... Line segment CD equal to the length of the segment ED... We measure the length of the segment with a compassED... We put the needle to the point E, lead the lead to the intersection with the radius. So we got the point C.
• Length of the segment DC - the side of the pentagram. We measure it, with the help of a compass we transfer it to a circle. To do this, with a compass with a delayed distance, we put four more points on the circle, connecting them in turn, we get a pentagram.

Here's what's interesting, if the vertices of the resulting pentagram are used to draw a star, it will consist of perfect triangles.

Application in construction

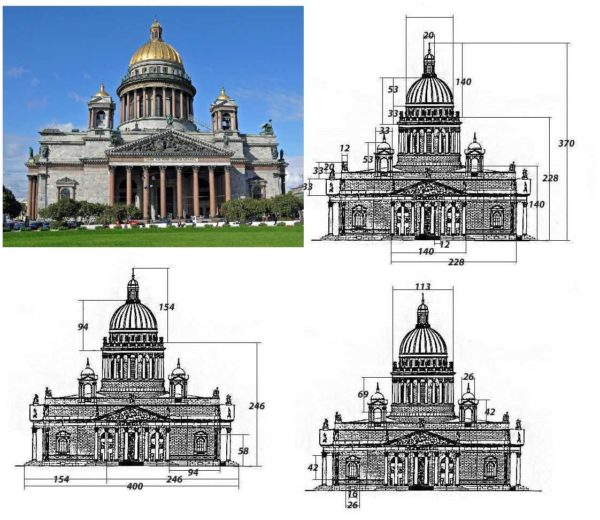
As already mentioned, it is not known who discovered the golden ratio, but everything that seems beautiful to us has exactly this aspect ratio. There are a lot of examples in nature. If we consider well-known buildings, then there is also the same pattern.

Isaac's Cathedral - you can count for fun

If you want your home inside and out to be attractive, remembered and liked, at least the basic proportions can be calculated when creating or choosing a project. It may not always be easy to make proportional adjustments and often involve additional costs. But, if, when creating a project, you immediately keep the golden ratio in mind, the questions themselves disappear. It's actually not that difficult.

For example, suppose you want a home of about 100 square meters. The long side can be taken up to 12 meters. Then the short one is 62% of the long and will be 7.44 meters. You can make 7 meters or 7.5, you can increase it to 8. Exact, up to a centimeter, compliance with the dimensions is not at all necessary. The ratio is important. And "by eye" even in the approach looks harmonious. The building area in this case is slightly smaller - 90-96 squares. If you need more, take the long side equal to 13 meters and count again. It seems like how to use the golden ratio when creating a house plan is understandable.

If the main parameters of the building are in the correct proportion, the building looks interesting in any style.

The floor height in this case is taken as 32% of the longest part. It will be 12 * 0.32 = 3.84 meters. In principle, this corresponds to the current ideas about the comfortable dimensions of the room, but if you wish, you can make the height smaller. All other fragments of the house are also calculated approximately.

Do not forget that the house must also fit into the landscape. If there is some kind of dominant - a high hill, for example, then it is necessary to calculate both the ratio with the hill and with the proportions of the plot. In general, in order to create a harmonious estate, many factors must be taken into account.

Not only straight lines can be used. True, it is more difficult to work with curved surfaces, and they cost more - a non-standard device is always more expensive

According to the same principle, they develop an internal layout, trying, if possible, to comply with the required ratio. But we will repeat once again: if possible. Don't get hung up on exact correspondence to the centimeter. The general trend is important.

Golden ratio in interior design

What else does the Golden Ratio provide besides visual enjoyment? Psychologists say that a person feels more comfortable in an interior created according to this rule. This is, of course, subjective, but you can try. So, here's how the golden ratio is interpreted in interior design:

• If you are going to divide the room into zones, use the rule. This means that one of the parts should be about 62%, the second - 38%.
• The area occupied by pieces of furniture should not be more than 2/3.
• When choosing furniture, we are guided by the rule: each medium-sized item belongs to large ones in the same way as small to medium ones.
• When choosing a color, follow approximately the same rules:
  • The main color is about 2/3, all additional and accent colors are 1/3. Colors are chosen to match according to certain rules.
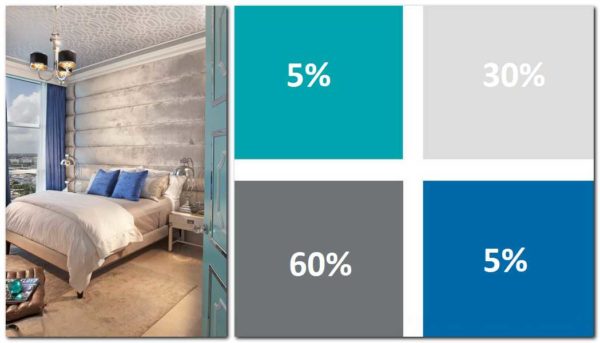
  • Second option: 60% is the main color, 30% is additional and 10% is accent.
    

    An example of color matching according to the rules of correct proportionality

• When using horizontal division of the wall (panel), the height of the panel can be taken as 1/3 or 2/3 of the total height of the room. But at the same time, furniture is selected proportional in height, and not in length.

Regarding furniture, the rule seems incomprehensible, but this is only at first glance. For example, we select a recreation group. A large object in this case is a sofa or sofa. Medium - coffee or coffee table, armchairs. Small ones - accessories. So, the dimensions of the coffee table should not be more than the long side of the sofa, the armchair - no more than its short side. Accessories are no larger than a table or chairs. Ideally, they correlate with them as 62% and 38%.

Proportionality is an important thing

Why is the exact ratio not indicated? Because, firstly, finding such items is unrealistic. Secondly, the golden ratio is not only 62% and 38%. It is also the Fibonacci sequence, following which also makes the design harmonious. There are people who have this sequence as a "built-in function". They do not need to count, they choose based on flair and intuition. But if you analyze their choice, the proportions will be close to ideal. Like this.

Golden ratio in landscape design

When creating a landscape on a site, the principle of ideal proportions is applied, calling it the triangle rule. The composition should have one dominant, the rest of its components only emphasize, set off it. For example, there is a large tree on the lot and you want to beat it. It will be the center of the composition - the dominant. Put it on a plan, line it up flower bed or rockery, rock garden - what you want to do.

The triangle rule in garden design

From the dominant plant or stone, draw two lines at right angles. Lower plants will need to be planted on these lines. Moreover, the second highest should not be higher than 2/3 of the height of the main object. The third object is no higher than 1/3. They complement the composition with even more stunted plantings. This is a quick guide to how to apply the golden ratio in planting planning.

But that's not all. Plants must be selected by color - a combination of greenery of different shades, blotches of flowers and decorative deciduous plants - everything obeys the same law. The dominant shade is about 60%, complementary colors - 30%, accents - 10%. This is if we talk about the rules of selection in one group. But it is also necessary to coordinate the whole plan as a whole - in size, height, colors.