Reglen om det gyldne forhold inden for arkitektur, konstruktion og design

Observationer af naturen og forsøg på at afdække hemmelighederne bag hendes smukke skabninger har bragt en masse opdagelser. En af dem er det gyldne forhold. Dette er et bestemt mønster, der adlyder alt, hvad vi kalder smukt. Mennesker, dyr, blomster, bygninger, galakser ...

Hvad er det gyldne forhold, og hvordan man forstår det

Ofte støder vi på huse, genstande, bygninger, planter, der fascinerer os med noget. Folk har længe forsøgt at forstå, hvorfor en ting synes os smuk, den anden ikke, de ledte efter mønstre. Og de ser ud til at have fundet det. Dette er et bestemt forhold mellem dele, der blev kaldt det gyldne forhold.

Om hvem og hvornår opfandt det gyldne forhold, ved ingen med sikkerhed. Nogen tilskriver opdagelsen til Pythagoras, men den første omtale blev fundet i "Elements" of Euclid, og han levede i det 3. århundrede f.Kr. Så fundet er helt klart gammelt. Det er på dette princip, at gamle græske og romerske templer blev bygget. Selvfølgelig kan disse være tilfældigheder, men de er meget mærkelige, og der er mange af dem. Så sandsynligvis var de opmærksomme på de ideelle proportioner.

Antikkenes overlevende bygninger er også underlagt det gyldne snit

Det er helt sikkert, at Leonardo da Vinci ledte efter bekræftelse af dette princip i menneskekroppens struktur. Og hvad der er mest interessant, jeg fandt det. De ansigter og kroppe, der synes smukke for os, har proportioner, der bare overholder loven om det gyldne forhold.

Den formelle definition lyder både enkel og kompleks. Det er forbundet med to segmenter i forskellige størrelser. Dette princip lyder sådan: Hvis et segment er opdelt i to ulige dele, vil denne opdeling være proportional, hvis det meste af segmentet vedrører helheden på samme måde som den mindre del til det større. Det bliver tydeligere, hvis du ser på illustrationen og formlen.

Princip og formel for det gyldne forhold

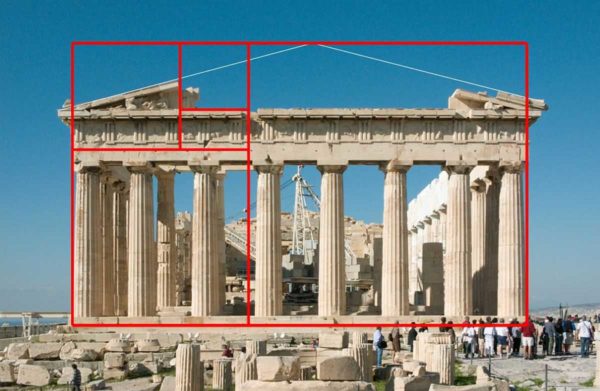
I figuren er hele segmentet opdelt, så hvis -en opdelt i b, vi får 1.1618, det samme tal opnås, hvis hele segmentet divideres med en stor del - -en... Dette tal er udførelsesformen for det ideelle forhold. Hvis du ser på billedet af Parthenon, overholder proportionerne af denne struktur også det angivne forhold.

Det samme mønster kan repræsenteres som procenter. Måske er det lettere for nogen. For at opdeling af helheden skal være proportional, skal delene være 62% og 38%. Det kan være lettere at huske på denne måde.

Fibonacci-sekvensen er ikke kun en matematisk formel

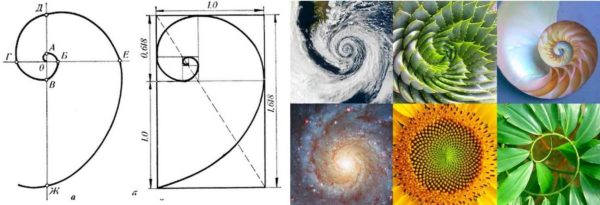
Dette mønster blev videreudviklet af matematikeren Fibonacci. Han udviklede en numerisk sekvens, hvis elementer fra den niende overholder den samme lov. Den grafiske gengivelse af denne sekvens er en spiral. Hvis du ser nøje, er der proportioner af skønhed i naturen, i arkitekturen og i den menneskelige krop.

Hvordan man bygger et rektangel med perfekte proportioner

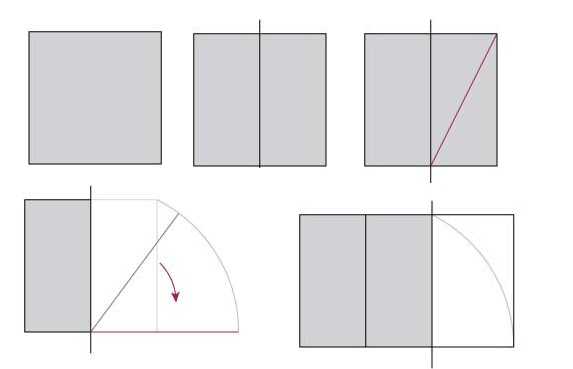
For at anvende de oplysninger, der modtages i praksis, skal man på en eller anden måde lære at opdele rummet eller bygge det i henhold til denne lov. Lad os først lære at bygge et rektangel med perfekte proportioner. Vi tager en firkant som basis.

Opretter et rektangel med et gyldent forhold

Del firkanten i to, træk en linje i en af ​​de resulterende rektangler, der forbinder de modsatte hjørner. Derefter tager vi et kompas, lægger en nål i midten af ​​firkantens nederste side, sætter længden af ​​den resulterende diagonal til side og markerer den på en linje, der vil være en fortsættelse af den nedre side af firkanten.Det resulterende rektangel har et billedformat på 1,62 (dette er nøjagtigt det forhold, der giver 62% og 38%).

Dette er tydeligvis ikke tilfældigt. Selvom ikke alt følger dette mønster

Hvad der er mere interessant er, at hvis du begynder at opdele 1.62-rektanglet i et kvadrat og et rektangel, får du igen et rektangel med perfekte proportioner, men mindre. Hvis du deler det igen efter det samme princip, vil der være et andet par firkant + rektangel med sider, hvis forhold svarer til det gyldne forhold. Og så videre, indtil du kan udføre divisionen. Men hvad der er endnu mere interessant, Fibonacci-serien passer perfekt ind i denne division, der ligner en afviklende spiral. Se illustrationen på billedet ovenfor.

Sådan opdeles et segment i henhold til reglen om det gyldne forhold

Denne færdighed vil være praktisk, fx når man opretter et husprojekt, planlægning, når man udvikler et lejlighedsdesign, arrangerer møbler osv. Det kan også være nødvendigt, når du planlægger et sted, blomsterbed, plantning af planter osv. Generelt kan den bruges næsten overalt.

Intet smukt, men du kan ikke tage øjnene af. Ved du hvorfor?

Så rækkefølgen for at opdele et segment i henhold til reglen for den gyldne sektion:

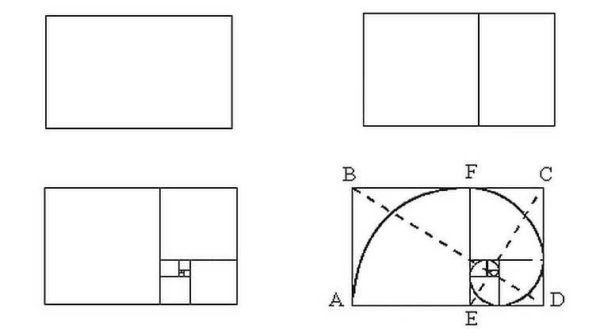
• Vi tager et segment, deler det i to.
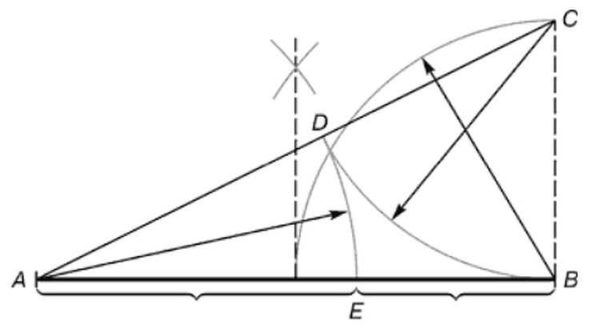
• Fra en af ​​enderne gendanner vi en vinkelret (lige linje i en vinkel på 90 °), som er halvdelen af ​​segmentets længde. I figuren er dette et segment F.Kr..
• Modtaget punkt C forbinde en lige linje med den anden ende af segmentet (EN).
• På segmentet AC sætte et punkt D... Det er placeret i en afstand svarende til segmentets længde F.Kr.... Den nemmeste måde at gøre dette på er med et kompas, men du kan også bruge en lineal.
• Vi måler længden af ​​segmentet AD (igen med et kompas eller en lineal). Vi udsætter den samme længde på segmentet AB... Vi forstår pointen E.
• Nu, hvis du måler længderne på segmenterne AE og EB og dele dem, får vi det samme eftertragtede nummer - 1.62.

Opdeling af et segment i sektioner med et ideelt forhold

Når du gentager proceduren et par gange, lærer du at gøre alt i bogstaveligt talt få minutter. Hvis du f.eks. Har brug for at bestemme vinduets højde og dens form, kan du også bruge disse proportioner. Efter det samme princip er det muligt at bestemme placeringen af ​​alle arkitektoniske elementer, deres størrelser. Når du planlægger eksisterende objekter, er det lettere at opdele ved hjælp af en procentdel. Her tæller du enten i dit hoved eller bruger en lommeregner.

Perfekt trekant og pentagram

En ligebenet trekant kaldes ideel, hvis bund henviser til sidelængden som 1/3. Det vil sige, igen observeres det gyldne forhold. Det er let at tegne en trekant med det perfekte billedformat. Det er mere praktisk med et kompas, men du kan klare dig med en lineal.

Den gyldne trekant, reglen om dets konstruktion og anvendelse i skabelsen af ​​et interiør, for eksempel

Konstruktionen er som følger. På en lige linje fra et punkt EN udsætte et segment med vilkårlig længde tre gange. Vi angiver denne længde O... Vi forstår pointen B... Træk en lige linje gennem den vinkelret på segmentet AB... På denne linje til begge sider af punktet B sæt værdien til side O... Vi får to point d og d1... Vi forbinder dem med en prik EN... Så vi fik en trekant, hvis sider er relaterede til 1,62. Du kan kontrollere dette, hvis du udsætter længden af ​​basen på den laterale side med et kompas (punkt C). Den anden kontrol er, at den modsatte vinkel er 36 °.

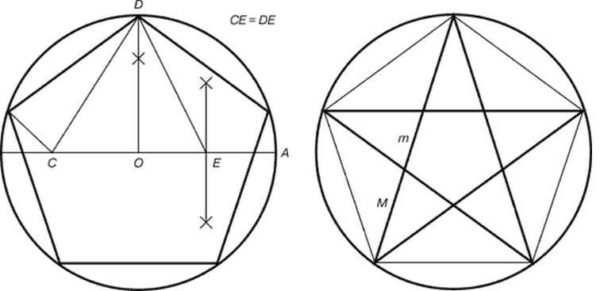
At bygge et pentagram er lidt mere kompliceret. Vi indskriver det i en cirkel, vi kan ikke undvære et kompas.

• Cirkelens centrum er betegnet med O, træk en lige linje gennem den, indtil den krydser cirklen. Et af skæringspunkterne er angivet EN... Linjestykke OA Er cirkelens diameter.
• Find midten af ​​segmentet OD, sæt et punkt E... Gendan lodret fra midten af ​​cirklen op til krydset med cirklen. Dette er pointen D.

Opbygning af et pentagram

• Forbind prikkerne E og D... Ved hjælp af et kompas udsætter vi et punkt på radius C... Linjestykke CD lig med længden af ​​segmentet ED... Vi måler segmentets længde med et kompasED... Vi sætter nålen på det punkt E, før ledningen til krydset med radius. Så vi fik pointen C.
• Segmentets længde DC - siden af ​​pentagrammet. Vi måler det ved hjælp af et kompas overfører vi det til en cirkel. For at gøre dette med et kompas med en forsinket afstand sætter vi fire flere punkter på cirklen, skiftevis forbinder dem, vi får et pentagram.

Her er hvad der er interessant, hvis hjørnerne i det resulterende pentagram bruges til at tegne en stjerne, vil det bestå af perfekte trekanter.

Anvendelse i byggeri

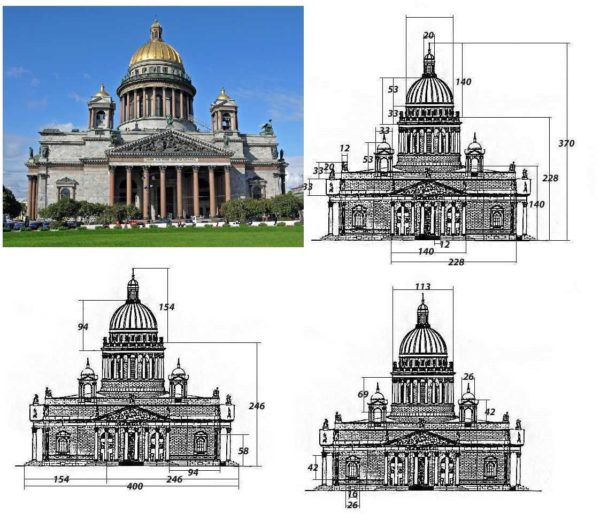
Som allerede nævnt vides det ikke, hvem der opdagede det gyldne forhold, men alt, hvad der virker smukt for os, har nøjagtigt dette billedformat. Der er mange eksempler i naturen. Hvis vi overvejer kendte bygninger, er der også det samme mønster.

Isaks katedral - du kan regne for sjov

Hvis du vil have dit hjem ude og ude til at være attraktivt, husket og lide, kan i det mindste de grundlæggende proportioner beregnes, når du opretter eller vælger et projekt. Det er ikke altid let at foretage forholdsmæssige justeringer og ofte medføre yderligere omkostninger. Men hvis du straks husker det gyldne forhold, når du opretter et projekt, forsvinder selve spørgsmålene. Det er faktisk ikke så svært.

Antag for eksempel, at du vil have et hjem på ca. 100 kvadratmeter. Langsiden kan tages op til 12 meter. Så er den korte 62% af den lange og vil være 7,44 meter. Du kan lave 7 meter eller 7,5, du kan øge det til 8. Præcis, op til en centimeter, overholdelse af dimensionerne er slet ikke nødvendigt. Forholdet er vigtigt. Og "med øjet" ser selv i tilgangen harmonisk ud. Bygningsområdet er i dette tilfælde lidt mindre - 90-96 firkanter. Hvis du har brug for mere, skal du tage den lange side svarende til 13 meter og tælle igen. Det ser ud til, hvordan man kan forstå det gyldne forhold, når man opretter en husplan.

Hvis bygningens hovedparametre er i det korrekte forhold, ser bygningen interessant ud i enhver stil.

Gulvhøjden tages i dette tilfælde som 32% af den længste del. Det vil være 12 * 0,32 = 3,84 meter. I princippet svarer dette til de nuværende ideer om rummets behagelige dimensioner, men hvis du ønsker det, kan du gøre højden mindre. Alle andre fragmenter af huset beregnes også omtrent.

Glem ikke, at huset også skal passe ind i landskabet. Hvis der er en slags dominerende - for eksempel en høj bakke, er det nødvendigt at beregne både forholdet med bakken og med plotens proportioner. Generelt skal der tages højde for mange faktorer for at skabe en harmonisk ejendom.

Ikke kun lige linjer kan bruges. Det er sandt, at det er sværere at arbejde med buede overflader, og de koster mere - en ikke-standard enhed er altid dyrere

Ifølge det samme princip udvikler de et internt layout, hvor de forsøger, hvis det er muligt, at overholde det krævede forhold. Men vi gentager igen: hvis det er muligt. Bliv ikke hængt op på nøjagtig korrespondance til centimeteren. Den generelle tendens er vigtig.

Gyldent forhold inden for interiørdesign

Hvad giver Golden Ratio ellers udover visuel nydelse? Psykologer siger, at en person føler sig mere komfortabel i et interiør skabt i henhold til denne regel. Dette er selvfølgelig subjektivt, men du kan prøve. Så her fortolkes det gyldne forhold i interiørdesign:

• Hvis du vil opdele rummet i zoner, skal du bruge reglen. Dette betyder, at en af ​​delene skal være omkring 62%, den anden - 38%.
• Området, der er besat af møbler, bør ikke være mere end 2/3.
• Når vi vælger møbler, styres vi af reglen: hvert mellemstykke med hensyn til dimensioner henviser til både store og små til mellemstore.
• Når du vælger en farve, skal du følge de samme regler:
  • Hovedfarven er ca. 2/3, alle ekstra farver og accentfarver er 1/3. Farver vælges til at matche i henhold til visse regler.
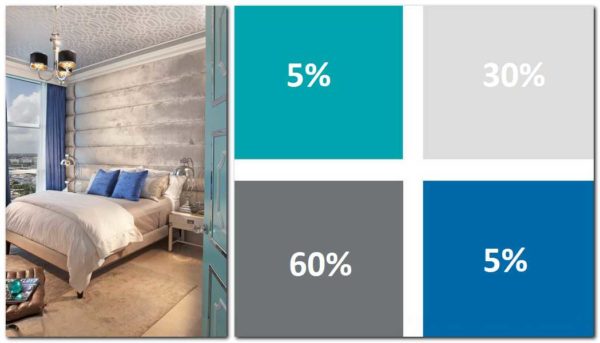
  • Anden mulighed: 60% er hovedfarven, 30% er ekstra og 10% er accent.
    

    Et eksempel på farvetilpasning i henhold til reglerne for korrekt proportionalitet

• Ved vandret opdeling af væggen (panelet) kan panelets højde tages som 1/3 eller 2/3 af rummets samlede højde. Men på samme tid vælges møbler proportionalt i højden og ikke i længden.

Med hensyn til møbler virker reglen uforståelig, men det er først ved første øjekast. For eksempel vælger vi en rekreativ gruppe. Et stort objekt i dette tilfælde er en sofa eller sofa. Medium - kaffe eller sofabord, lænestole. Små - tilbehør. Så sofabordets dimensioner bør ikke være mere end sofaens lange side, lænestolen - ikke mere end dens korte side. Tilbehør er ikke større end et bord eller stole. Ideelt set korrelerer de med dem som 62% og 38%.

Proportionalitet er en vigtig ting

Hvorfor er det nøjagtige forhold ikke angivet? Fordi det for det første er urealistisk at finde sådanne ting. For det andet er det gyldne forhold ikke kun 62% og 38%. Det er også Fibonacci-sekvensen, hvorefter designet også gør designet harmonisk. Der er mennesker, der har denne sekvens som en "indbygget funktion". De behøver ikke at tælle, de vælger ud fra flair og intuition. Men hvis du analyserer deres valg, vil proportionerne være tæt på ideelle. Sådan her.

Gyldent forhold i landskabsdesign

Når du opretter et landskab på et sted, anvendes princippet om ideelle proportioner og kalder det trekantreglen. Sammensætningen skal have en dominerende, resten af ​​dens komponenter understreger kun, modregner det. For eksempel er der et stort træ på partiet, og du vil slå det. Det vil være centrum for kompositionen - den dominerende. Sæt det på en plan, sæt den op blomsterseng eller sten, stenhave - hvad du vil gøre.

Trekantreglen i havedesign

Fra den dominerende plante eller sten tegner du to linjer vinkelret. Lavere planter skal plantes på disse linjer. Desuden bør den næsthøjeste ikke være højere end 2/3 af hovedobjektets højde. Det tredje objekt er ikke højere end 1/3. De supplerer sammensætningen med endnu mere stuntede beplantninger. Dette er en hurtig guide til, hvordan man anvender det gyldne forhold i planteplanlægning.

Men det er ikke alt. Planter skal vælges efter farve - en kombination af grønt i forskellige nuancer, pletter af blomster og dekorative løvfældende planter - alt adlyder den samme lov. Den dominerende skygge er omkring 60%, komplementære farver - 30%, accenter - 10%. Dette er, hvis vi taler om reglerne for udvælgelse i en gruppe. Men det er også nødvendigt at koordinere hele planen som helhed - i størrelse, højde, farver.