Ang tuntunin ng ginintuang ratio sa arkitektura, konstruksyon at disenyo
Ang mga pagmamasid sa kalikasan at pagtatangka upang alisan ng takip ang mga lihim ng mga magagandang nilalang ay nagdala ng maraming pagtuklas. Ang isa sa mga ito ay ang gintong ratio. Ito ay isang tiyak na pattern na sumusunod sa lahat ng tinatawag nating maganda. Mga tao, hayop, bulaklak, gusali, kalawakan ...
Ang nilalaman ng artikulo
- 1 Ano ang gintong ratio at kung paano ito mauunawaan
- 2 Paano bumuo ng isang rektanggulo na may perpektong mga sukat
- 3 Paano hatiin ang isang segment ayon sa panuntunan ng ginintuang ratio
- 4 Perpektong tatsulok at pentagram
- 5 Application sa konstruksyon
- 6 Gintong ratio sa panloob na dekorasyon
- 7 Ang gintong ratio sa disenyo ng landscape
Ano ang gintong ratio at kung paano ito mauunawaan
Kadalasan ay nakakakita tayo ng mga bahay, bagay, gusali, halaman na nakakaakit sa atin ng isang bagay. Matagal nang sinubukan ng mga tao na maunawaan kung bakit ang isang bagay ay tila maganda sa amin, ang isa pa ay hindi, naghahanap sila ng mga pattern. At tila natagpuan nila ito. Ito ay isang tiyak na ratio ng mga bahagi, na tinawag na golden ratio.
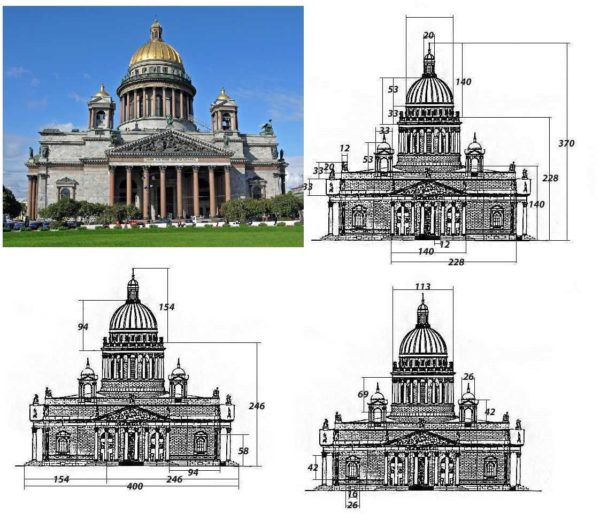
Walang siguradong nakakaalam kung sino at kailan ang naimbento ang gintong ratio. Ang isang tao ay nagpatungkol sa pagtuklas kay Pythagoras, ngunit ang unang pagbanggit ay natagpuan sa "Mga Sangkap" ng Euclid, at siya ay nabuhay noong ika-3 siglo BC. Kaya't ang hanapin ay malinaw na luma na. Sa prinsipyong ito na itinayo ang mga sinaunang Greek at Roman na templo. Siyempre, maaaring ito ay nagkataon, ngunit ang mga ito ay napaka-kakaiba at maraming mga ito. Kaya malamang na alam nila ang perpektong mga sukat.
Ang mga natitirang mga gusali ng unang panahon ay napapailalim din sa patakaran ng ginintuang seksyon
Ito ay ganap na natitiyak na si Leonardo da Vinci ay naghahanap ng kumpirmasyon ng prinsipyong ito sa istraktura ng katawan ng tao. At, kung ano ang pinaka-kagiliw-giliw, nahanap ko ito. Ang mga mukha at katawan na mukhang maganda sa amin ay may mga sukat na sumusunod lamang sa batas ng golden ratio.
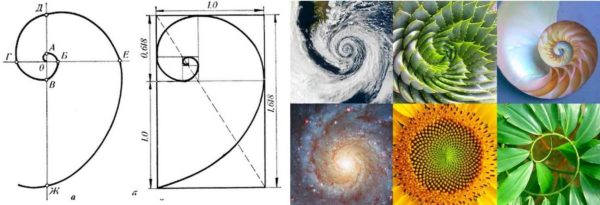
Ang pormal na kahulugan ay tunog parehong simple at kumplikado. Nauugnay ito sa dalawang segment na magkakaibang laki. Ang prinsipyong ito ay may tunog na katulad nito: kung ang isang segment ay nahahati sa dalawang hindi pantay na bahagi, kung gayon ang paghati na ito ay proporsyonal kung ang karamihan sa segment ay tumutukoy sa kabuuan sa parehong paraan tulad ng mas maliit na bahagi sa mas malaki. Mas magiging malinaw kung titingnan mo ang ilustrasyon at ang pormula.
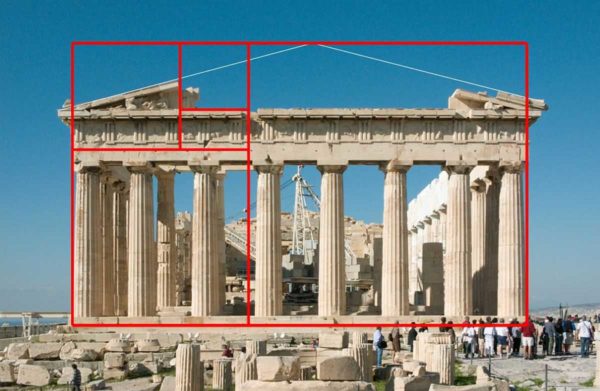
Sa pigura, nahahati ang buong segment upang kung a hatiin sa b, nakakuha kami ng 1.1618, ang parehong pigura ay nakuha kung ang buong segment ay nahahati sa isang malaking bahagi - a... Ang bilang na ito ay ang sagisag ng perpektong proporsyon. Ngayon, kung titingnan mo ang larawan ng Parthenon, ang mga proporsyon ng istrakturang ito ay sumusunod din sa ipinahiwatig na ratio.
Ang parehong pattern ay maaaring kinatawan bilang mga porsyento. Mas madali siguro para sa isang tao. Upang maging proporsyonal ang paghahati ng kabuuan, ang mga bahagi ay dapat na 62% at 38%. Maaaring mas madaling matandaan ang ganitong paraan.
Ang pattern na ito ay binuo pa ng dalub-agbilang Fibonacci. Bumuo siya ng isang pagkakasunud-sunod ng bilang, ang mga elemento kung saan, simula sa ikasiyam, sumunod sa parehong batas. Ang graphic na representasyon ng pagkakasunud-sunod na ito ay isang spiral. Kung titingnan mo nang mabuti, may mga proporsyon ng kagandahan sa kalikasan, sa arkitektura, at sa katawan ng tao.
Paano bumuo ng isang rektanggulo na may perpektong mga sukat
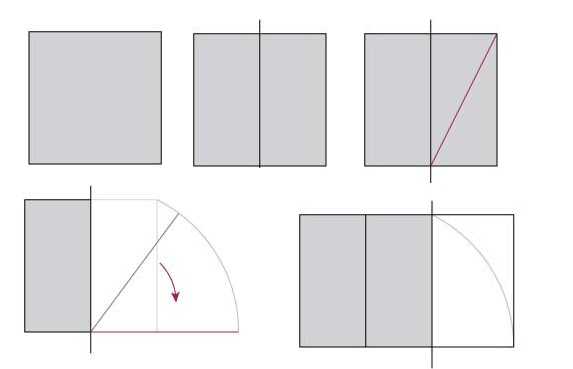
Upang mailapat ang impormasyong natanggap sa pagsasagawa, dapat kahit papaano matuto ang isang tao na hatiin ang puwang o itayo ito alinsunod sa batas na ito. Una, alamin natin kung paano bumuo ng isang rektanggulo na may perpektong proporsyon. Kumuha kami ng isang parisukat bilang batayan.
Hatiin ang parisukat sa kalahati, gumuhit ng isang linya sa isa sa mga nagresultang mga parihaba na nag-uugnay sa kabaligtaran na mga sulok. Pagkatapos kumuha kami ng isang kumpas, maglagay ng karayom sa gitna ng ibabang bahagi ng parisukat, itabi ang haba ng nagresultang dayagonal at markahan ito sa isang linya na magiging pagpapatuloy ng mas mababang bahagi ng parisukat.Ang nagresultang rektanggulo ay may isang aspeto ng ratio na 1.62 (ito mismo ang eksaktong ratio na nagbibigay ng 62% at 38%).
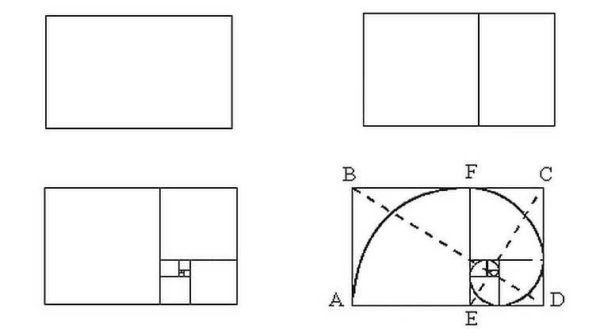
Ano ang mas kawili-wili ay kung sinimulan mong hatiin ang 1.62 na rektanggulo sa isang parisukat at isang rektanggulo, makakakuha ka muli ng isang rektanggulo na may perpektong mga sukat, ngunit mas maliit. Kung hatiin mo ulit ito alinsunod sa parehong prinsipyo, magkakaroon ng isa pang pares ng parisukat + parihaba na may mga gilid, ang ratio na kung saan ay tumutugma sa gintong ratio. At iba pa hanggang sa maisagawa mo ang paghahati. Ngunit kung ano ang mas kawili-wili, ang serye ng Fibonacci ay ganap na umaangkop sa dibisyon na ito, na mukhang isang pag-iwas ng spiral. Tingnan ang ilustrasyon sa larawan sa itaas.
Paano hatiin ang isang segment ayon sa panuntunan ng ginintuang ratio
Ang kasanayang ito ay kapaki-pakinabang, halimbawa, kapag lumilikha ng isang proyekto sa bahay, pagpaplano, kapag bumubuo ng isang disenyo ng apartment, pag-aayos ng mga kasangkapan, atbp. Maaaring kailanganin din ito kapag nagpaplano ng isang site, mga bulaklak na kama, pagtatanim ng mga halaman, atbp. Sa pangkalahatan, maaari itong magamit halos saanman.
Kaya, ang pagkakasunud-sunod ng paghati ng isang segment ayon sa panuntunan ng ginintuang seksyon:
- Kumuha kami ng isang segment, hatiin ito sa kalahati.
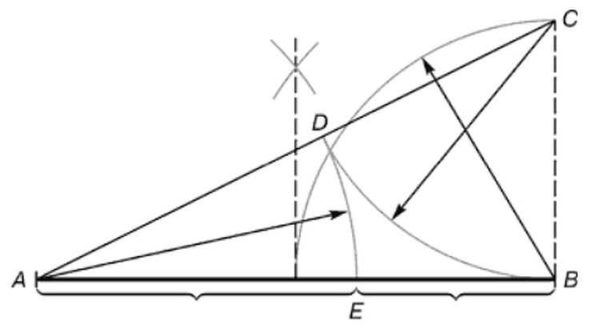
- Mula sa isa sa mga dulo ibabalik namin ang isang patayo (tuwid na linya sa isang anggulo ng 90 °), na kalahati ng haba ng segment. Sa pigura, ito ay isang segment BC.
- Natanggap na point C ikonekta ang isang tuwid na linya sa kabilang dulo ng segment (A).
- Sa segment AC maglagay ng isang punto D... Matatagpuan ito sa isang distansya na katumbas ng haba ng segment BC... Ang pinakamadaling paraan upang gawin ito ay sa isang compass, ngunit maaari mo ring gamitin ang isang pinuno.
- Sinusukat namin ang haba ng segment AD (muli sa isang compass, o isang pinuno). Ipinagpaliban namin ang parehong haba sa segment AB... Nakukuha natin ang punto E.
- Ngayon, kung susukatin mo ang haba ng mga segment AE at EB at hatiin ang mga ito, nakakakuha kami ng parehong nais na numero - 1.62.
Ang pag-uulit ng pamamaraan ng ilang beses, matututunan mo kung paano gawin ang lahat nang literal nang ilang minuto. Kung kailangan mo, halimbawa, upang matukoy ang taas ng window, ang hugis nito, maaari mo ring gamitin ang mga proporsyon na ito. Sa pamamagitan ng parehong prinsipyo, posible na matukoy ang lokasyon ng lahat ng mga elemento ng arkitektura, ang kanilang laki. Kapag nagpaplano ng mga mayroon nang bagay, mas madaling hatiin sa pamamagitan ng paggamit ng isang porsyento. Dito maaari mong bilangin sa iyong ulo, o gumamit ng isang calculator.
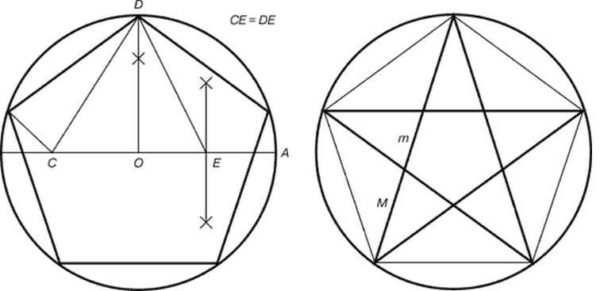
Perpektong tatsulok at pentagram
Ang isang tatsulok na isosceles ay tinatawag na perpekto, ang base nito ay tumutukoy sa haba ng gilid bilang 1/3. Iyon ay, muli ang ginintuang ratio ay sinusunod. Madaling gumuhit ng isang tatsulok na may perpektong ratio ng aspeto. Ito ay mas maginhawa sa isang compass, ngunit maaari kang makakuha ng isang pinuno.

Ang gintong tatsulok, ang panuntunan sa pagtatayo at aplikasyon nito sa paglikha ng isang panloob, halimbawa
Ang konstruksyon ay ang mga sumusunod. Sa isang tuwid na linya mula sa isang punto A ipagpaliban ang isang segment ng di-makatwirang haba ng tatlong beses. Tinukoy namin ang haba na ito O... Nakukuha natin ang punto B... Gumuhit ng isang tuwid na linya sa pamamagitan nito, patayo sa segment AB... Sa linyang ito sa magkabilang panig ng punto B itabi ang halaga O... Nakukuha namin ang dalawang puntos d at d1... Ikonekta namin ang mga ito sa isang tuldok A... Nakuha namin ang isang tatsulok, ang mga panig nito ay nauugnay bilang 1.62. Maaari mong suriin ito kung ipagpaliban mo ang haba ng base sa lateral na bahagi na may isang compass (point C). Ang pangalawang tseke ay ang kabaligtaran na anggulo ay 36 °.
Ang pagbuo ng isang pentagram ay medyo kumplikado. Isinulat namin ito sa isang bilog, hindi namin magagawa nang walang isang compass.
- Ang gitna ng bilog ay tinukoy ng O, gumuhit ng isang tuwid na linya sa pamamagitan nito hanggang sa lumusot ito sa bilog. Ang isa sa mga puntos ng intersection ay naipahiwatig A... Segment ng linya OA naman Ay ang diameter ng bilog.
- Hanapin ang gitna ng segment OD, maglagay ng isang punto E... Ibalik ang patayo mula sa gitna ng bilog hanggang sa intersection ng bilog. Ito ang punto D.
- Ikonekta ang mga tuldok E at D... Sa tulong ng isang compass, ipinagpaliban namin ang punto C... Segment ng linya CD katumbas ng haba ng segment ED... Sinusukat namin ang haba ng segment gamit ang isang compassED... Inilalagay namin ang karayom sa punto E, pangunahan ang tingga sa intersection na may radius. Kaya nakuha namin ang punto C.
- Haba ng segment DC - ang gilid ng pentagram. Sinusukat namin ito, sa tulong ng isang compass inililipat namin ito sa isang bilog. Upang gawin ito, sa isang compass na may isang naantala na distansya, naglalagay kami ng apat na higit pang mga puntos sa bilog, na kinokonekta sa kanila sa pagliko, nakakakuha kami ng isang pentagram.
Narito kung ano ang kagiliw-giliw, kung ang mga vertex ng nagresultang pentagram ay ginagamit upang gumuhit ng isang bituin, ito ay binubuo ng mga perpektong triangles.
Application sa konstruksyon
Tulad ng nabanggit na, hindi alam kung sino ang natuklasan ang gintong ratio, ngunit ang lahat na tila maganda sa amin ay may eksaktong aspeto ng ratio na ito. Mayroong maraming mga halimbawa sa kalikasan. Kung isasaalang-alang natin ang mga kilalang gusali, magkakaroon din ng parehong pattern.
Kung nais mong ang iyong bahay sa loob at labas ay maging kaakit-akit, maalala at magustuhan, hindi bababa sa mga pangunahing sukat ay maaaring kalkulahin kapag lumilikha o pumili ng isang proyekto. Maaaring hindi laging madali ang gumawa ng mga proporsyonal na pagsasaayos at madalas na nagsasangkot ng mga karagdagang gastos. Ngunit, kung, kapag lumilikha ng isang proyekto, agad mong itatago ang gintong ratio, ang mga katanungan mismo ay nawawala. Talagang hindi ito mahirap.
Halimbawa, ipagpalagay na gusto mo ng bahay na halos 100 metro kuwadradong. Ang mahabang bahagi ay maaaring makuha hanggang sa 12 metro. Pagkatapos ang maikling isa ay 62% ng haba at magiging 7.44 metro. Maaari kang gumawa ng 7 metro o 7.5, maaari mo itong dagdagan sa 8. Eksakto, hanggang sa isang sentimetro, ang pagsunod sa mga sukat ay hindi kinakailangan. Mahalaga ang ratio. At ang "by eye" kahit na sa paglapit ay mukhang maayos. Ang lugar ng gusali sa kasong ito ay bahagyang mas maliit - 90-96 mga parisukat. Kung kailangan mo ng higit pa, kunin ang mahabang bahagi na katumbas ng 13 metro at bilangin muli. Tila tulad ng kung paano gamitin ang gintong ratio kapag ang paglikha ng isang plano sa bahay ay naiintindihan.

Kung ang pangunahing mga parameter ng gusali ay nasa tamang proporsyon, ang gusali ay mukhang kawili-wili sa anumang istilo.
Ang taas ng sahig sa kasong ito ay kinuha bilang 32% ng pinakamahabang bahagi. Magiging 12 * 0.32 = 3.84 metro. Sa prinsipyo, tumutugma ito sa kasalukuyang mga ideya tungkol sa mga komportableng sukat ng silid, ngunit kung nais mo, maaari mong gawing mas maliit ang taas. Ang lahat ng iba pang mga fragment ng bahay ay kinakalkula din ng humigit-kumulang.
Huwag kalimutan na ang bahay ay dapat ding magkasya sa tanawin. Kung mayroong ilang uri ng nangingibabaw - isang mataas na burol, halimbawa, pagkatapos ay kinakailangan upang makalkula ang parehong ratio sa burol at sa mga proporsyon ng isang lagay ng lupa. Sa pangkalahatan, upang lumikha ng isang maayos na estate, maraming mga kadahilanan ang dapat isaalang-alang.

Hindi lamang mga tuwid na linya ang maaaring magamit. Totoo, mas mahirap na gumana sa mga hubog na ibabaw, at nagkakahalaga sila ng mas malaki - ang isang hindi pamantayang aparato ay palaging mas mahal
Ayon sa parehong prinsipyo, nagkakaroon sila ng panloob na layout, sinusubukan, kung maaari, na sumunod sa kinakailangang ratio. Ngunit uulitin natin muli: kung maaari. Huwag mabitin sa eksaktong pagsulat sa sentimeter. Ang pangkalahatang kalakaran ay mahalaga.
Gintong ratio sa panloob na dekorasyon
Ano pa ang ibinibigay ng Golden Ratio bukod sa visual na kasiyahan? Sinasabi ng mga psychologist na ang isang tao ay mas komportable sa looban na nilikha alinsunod sa panuntunang ito. Ito ay, siyempre, paksa, ngunit maaari mong subukan. Kaya, narito kung paano ang interpretasyong ginto ay binibigyang kahulugan sa panloob na disenyo:
- Kung hahatiin mo ang silid sa mga zone, gamitin ang panuntunan. Nangangahulugan ito na ang isa sa mga bahagi ay dapat na tungkol sa 62%, ang iba pa - 38%.
- Ang lugar na inookupahan ng mga piraso ng kasangkapan ay hindi dapat higit sa 2/3.
- Kapag pumipili ng mga kasangkapan sa bahay, gagabayan kami ng panuntunan: ang bawat item na may katamtamang sukat ay kabilang sa malalaki sa parehong paraan tulad ng maliit hanggang sa daluyan.
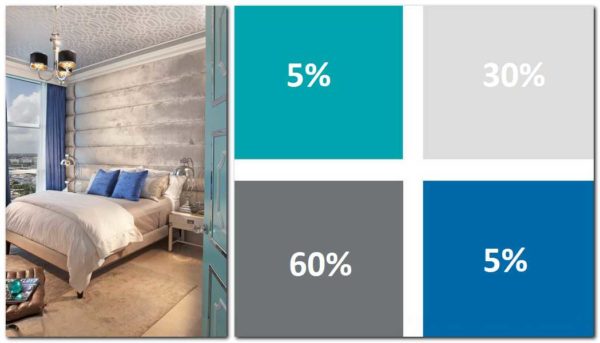
- Kapag pumipili ng isang kulay, sundin ang halos parehong mga patakaran:
- Ang pangunahing kulay ay tungkol sa 2/3, ang lahat ng mga karagdagang at accent na kulay ay 1/3. Ang mga kulay ay pinili upang tumugma alinsunod sa ilang mga patakaran.
- Pangalawang pagpipilian: 60% ang pangunahing kulay, 30% ay karagdagang at 10% ang tuldik.
- Kapag gumagamit ng pahalang na paghahati ng pader (panel), ang taas ng panel ay maaaring makuha bilang 1/3 o 2/3 ng kabuuang taas ng silid. Ngunit sa parehong oras, ang kasangkapan sa bahay ay napili proporsyonal sa taas, at hindi sa haba.
Tungkol sa mga kasangkapan sa bahay, ang panuntunan ay tila hindi maintindihan, ngunit ito ay sa unang tingin lamang. Halimbawa, pumili kami ng isang pangkat ng libangan. Ang isang malaking bagay sa kasong ito ay isang sofa o sofa. Katamtaman - mesa ng kape o kape, mga armchair. Maliit - mga accessories. Kaya, ang mga sukat ng talahanayan ng kape ay hindi dapat higit sa mahabang bahagi ng sofa, ang armchair - hindi hihigit sa maikling gilid nito. Ang mga accessories ay hindi mas malaki kaysa sa isang mesa o upuan. Sa isip, nakikipag-ugnayan sila sa kanila bilang 62% at 38%.
Bakit hindi ipinahiwatig ang eksaktong ratio? Sapagkat, una, ang paghahanap ng mga nasabing item ay hindi makatotohanang. Pangalawa, ang gintong ratio ay hindi lamang 62% at 38%. Ito rin ang pagkakasunud-sunod ng Fibonacci, na sinusundan na gumagawa din ng maayos na disenyo. Mayroong mga tao na mayroong pagkakasunud-sunod na ito bilang isang "built-in na function". Hindi nila kailangang bilangin, pipiliin sila batay sa talino at intuwisyon. Ngunit kung pag-aralan mo ang kanilang pagpipilian, ang mga proporsyon ay malapit sa perpekto. Ganito.
Gintong ratio sa disenyo ng tanawin
Kapag lumilikha ng isang tanawin sa isang site, ang prinsipyo ng perpektong proporsyon ay inilalapat, tinawag itong patakaran ng tatsulok. Ang komposisyon ay dapat magkaroon ng isang nangingibabaw, ang natitirang mga bahagi nito ay binibigyang diin lamang, lilim ito. Halimbawa, mayroong isang malaking puno sa lote at nais mong talunin ito. Ito ang magiging sentro ng komposisyon - ang nangingibabaw. Ilagay ito sa isang plano, ihanay ito taniman ng bulaklak o rockery, rock hardin - kung ano ang nais mong gawin.
Mula sa nangingibabaw na halaman o bato, gumuhit ng dalawang linya sa tamang mga anggulo. Ang mga mas mababang halaman ay kailangang itanim sa mga linyang ito. Bukod dito, ang pangalawang pinakamataas ay hindi dapat mas mataas sa 2/3 ng taas ng pangunahing bagay. Ang pangatlong bagay ay hindi mas mataas sa 1/3. Pinupunan nila ang komposisyon na may mas maraming mga stunted plantings. Ito ay isang mabilis na gabay sa kung paano ilapat ang golden ratio sa pagpaplano ng pagtatanim.
Ngunit hindi lang iyon. Ang mga halaman ay dapat mapili ng kulay - isang kombinasyon ng mga halaman ng iba't ibang mga shade, blotches ng mga bulaklak at pandekorasyon nangungulag halaman - lahat ng bagay ay sumusunod sa parehong batas. Ang nangingibabaw na lilim ay tungkol sa 60%, mga pantulong na kulay - 30%, mga accent - 10%. Ito ay kung pag-uusapan natin ang tungkol sa mga patakaran ng pagpili sa isang pangkat. Ngunit kinakailangan ding iugnay ang buong plano bilang isang buo - sa laki, taas, kulay.