Peraturan nisbah emas dalam seni bina, pembinaan dan reka bentuk
Pemerhatian terhadap alam semula jadi dan percubaan untuk membongkar rahsia makhluk cantiknya telah banyak membawa penemuan. Salah satunya adalah nisbah keemasan. Ini adalah corak tertentu yang mematuhi semua yang kita sebut cantik. Orang, haiwan, bunga, bangunan, galaksi ...
Kandungan artikel
- 1 Apakah nisbah keemasan dan bagaimana memahaminya
- 2 Cara membina segi empat tepat dengan bahagian yang sempurna
- 3 Cara membahagi segmen mengikut peraturan nisbah keemasan
- 4 Segitiga dan pentagram sempurna
- 5 Permohonan dalam pembinaan
- 6 Nisbah emas dalam reka bentuk dalaman
- 7 Nisbah keemasan dalam reka bentuk landskap
Apakah nisbah keemasan dan bagaimana memahaminya
Selalunya kita menjumpai rumah, objek, bangunan, tumbuh-tumbuhan yang memikat kita dengan sesuatu. Orang telah lama berusaha memahami mengapa satu perkara kelihatan indah bagi kita, yang lain tidak, mereka mencari corak. Dan mereka sepertinya telah menjumpainya. Ini adalah nisbah bahagian tertentu, yang disebut nisbah emas.
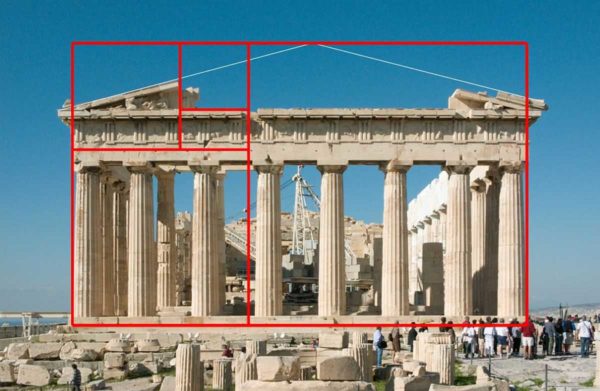
Tidak ada yang tahu pasti siapa dan kapan mencipta nisbah keemasan. Seseorang mengaitkan penemuan itu dengan Pythagoras, tetapi sebutan pertama dijumpai dalam "Elemen" Euclid, dan dia hidup pada abad ke-3 SM. Jadi penemuan itu jelas lama. Berdasarkan prinsip inilah kuil-kuil Yunani dan Rom kuno dibina. Sudah tentu, ini mungkin kebetulan, tetapi sangat pelik dan terdapat banyak perkara. Jadi kemungkinan besar mereka mengetahui perkadaran yang ideal.
Sudah pasti bahawa Leonardo da Vinci sedang mencari pengesahan prinsip ini dalam struktur tubuh manusia. Dan, yang paling menarik, saya dapati. Wajah dan badan yang kelihatan cantik bagi kita mempunyai perkadaran yang hanya mematuhi hukum nisbah keemasan.
Definisi formal kedengaran sederhana dan kompleks. Ia dikaitkan dengan dua segmen dengan ukuran yang berbeza. Prinsip ini terdengar seperti ini: jika segmen dibahagikan kepada dua bahagian yang tidak sama, maka pembahagian ini akan berkadaran jika sebahagian besar segmen merujuk kepada keseluruhan dengan cara yang sama dengan bahagian yang lebih kecil hingga yang lebih besar. Akan lebih jelas jika anda melihat ilustrasi dan formula.
Dalam rajah tersebut, keseluruhan segmen dibahagi sehingga jika a berpecah menjadi b, kita mendapat 1.1618, angka yang sama diperoleh jika keseluruhan segmen dibahagi dengan sebahagian besar - a... Nombor ini adalah penjelmaan bagi bahagian ideal. Sekarang, jika anda melihat gambar Parthenon, bahagian struktur ini juga mematuhi nisbah yang ditunjukkan.
Corak yang sama dapat ditunjukkan sebagai peratusan. Mungkin lebih senang bagi seseorang. Agar pembahagian keseluruhannya berkadaran, bahagiannya mestilah 62% dan 38%. Mungkin lebih mudah untuk mengingatnya dengan cara ini.
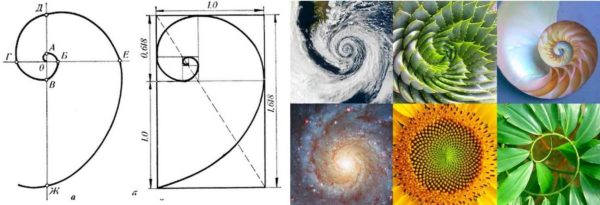
Corak ini dikembangkan lagi oleh ahli matematik Fibonacci. Dia mengembangkan urutan berangka, unsur-unsurnya, bermula dari kesembilan, mematuhi undang-undang yang sama. Perwakilan grafik urutan ini adalah lingkaran. Sekiranya anda melihat dengan teliti, terdapat sebilangan besar keindahan alam, seni bina, dan tubuh manusia.
Cara membina segi empat tepat dengan bahagian yang sempurna
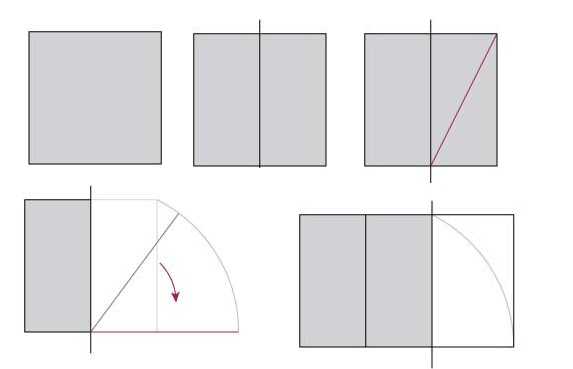
Untuk menerapkan maklumat yang diterima dalam praktik, seseorang harus belajar membahagikan ruang atau membinanya mengikut undang-undang ini. Pertama, mari belajar bagaimana membina segi empat tepat dengan perkadaran yang sempurna. Kami mengambil petak sebagai asas.
Bahagikan petak menjadi dua, lukis garis di salah satu segi empat tepat yang terhasil yang menghubungkan sudut yang bertentangan. Kemudian kami mengambil kompas, meletakkan jarum di tengah-tengah sisi bawah alun-alun, mengetepikan panjang pepenjuru yang dihasilkan dan menandakannya pada garis yang akan menjadi lanjutan dari sisi bawah alun-alun.Segi empat tepat yang dihasilkan mempunyai nisbah aspek 1.62 (ini adalah nisbah tepat yang memberikan 62% dan 38%).
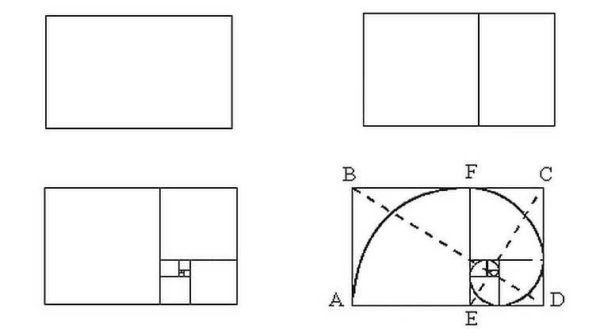
Apa yang lebih menarik ialah jika anda mula membahagikan segiempat tepat 1.62 menjadi segi empat sama dan segi empat tepat, anda akan mendapat satu lagi segi empat tepat dengan perkadaran yang sempurna, tetapi lebih kecil. Sekiranya anda membahagikannya lagi mengikut prinsip yang sama, akan ada sepasang persegi + segi empat dengan sisi lain, nisbahnya akan sesuai dengan nisbah keemasan. Dan seterusnya sehingga anda dapat menjalankan pembahagian. Tetapi yang lebih menarik lagi, siri Fibonacci sangat sesuai dengan bahagian ini, yang kelihatan seperti lingkaran yang tidak menenangkan. Lihat ilustrasi dalam gambar di atas.
Cara membahagi segmen mengikut peraturan nisbah keemasan
Kemahiran ini akan sangat berguna, misalnya, ketika membuat projek rumah, merancang, ketika mengembangkan reka bentuk pangsapuri, mengatur perabot, dll. Mungkin juga diperlukan ketika merancang sebuah lokasi, tempat tidur bunga, menanam tanaman, dll. Secara amnya, ia boleh digunakan hampir di mana sahaja.
Jadi, urutan membahagi segmen mengikut peraturan bahagian emas:
- Kami mengambil segmen, bahagikan kepada dua.
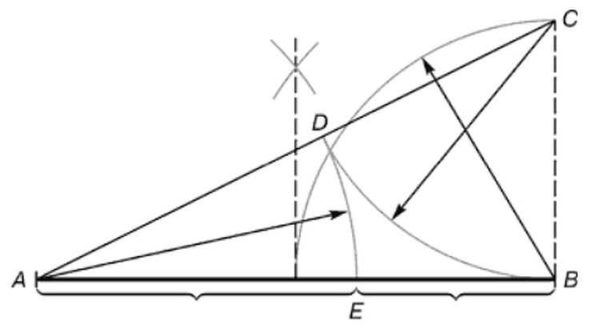
- Dari salah satu hujungnya kita mengembalikan tegak lurus (garis lurus pada sudut 90 °), yang merupakan separuh panjang segmen. Dalam gambar, ini adalah segmen SM.
- Titik diterima C sambungkan garis lurus dengan hujung segmen yang lain (A).
- Di segmen AC meletakkan titik D... Ia terletak pada jarak yang sama dengan panjang segmen SM... Cara termudah untuk melakukannya adalah dengan kompas, tetapi anda juga boleh menggunakan pembaris.
- Kami mengukur panjang segmen IKLAN (sekali lagi dengan kompas, atau pembaris). Kami menangguhkan panjang yang sama pada segmen AB... Kami mendapat intinya E.
- Sekarang, jika anda mengukur panjang segmen AE dan EB dan bahagikannya, kita mendapat nombor yang didambakan yang sama - 1.62.
Mengulangi prosedur beberapa kali, anda akan belajar bagaimana melakukan semuanya dalam beberapa minit. Sekiranya anda memerlukan, misalnya, untuk menentukan ketinggian tingkap, bentuknya, anda juga boleh menggunakan perkadaran ini. Dengan prinsip yang sama, adalah mungkin untuk menentukan lokasi semua elemen seni bina, ukurannya. Semasa merancang objek yang ada, lebih mudah dibahagi dengan menggunakan peratusan. Di sini anda boleh mengira, atau menggunakan kalkulator.
Segitiga dan pentagram sempurna
Segitiga isoseles disebut ideal, pangkalnya merujuk kepada panjang sisi sebagai 1/3. Iaitu, sekali lagi nisbah keemasan diperhatikan. Sangat mudah untuk melukis segitiga dengan nisbah aspek yang sempurna. Lebih mudah menggunakan kompas, tetapi anda boleh mendapatkannya dengan pembaris.
Pembinaannya adalah seperti berikut. Pada garis lurus dari satu titik A menangguhkan segmen panjang sewenang-wenang tiga kali. Kami menunjukkan panjang ini O... Kami mendapat intinya B... Lukis garis lurus melaluinya, berserenjang dengan segmen AB... Pada garis ini ke kedua-dua sisi titik B ketepikan nilai O... Kami mendapat dua mata d dan d1... Kami menghubungkannya dengan titik A... Oleh itu, kami mendapat segitiga, sisi-sisinya berkait sebagai 1.62. Anda boleh memeriksa ini jika anda menangguhkan panjang pangkal di sisi sisi dengan kompas (titik C). Pemeriksaan kedua adalah bahawa sudut yang bertentangan adalah 36 °.
Membina pentagram sedikit lebih rumit. Kita menuliskannya dalam bulatan, kita tidak dapat melakukannya tanpa kompas.
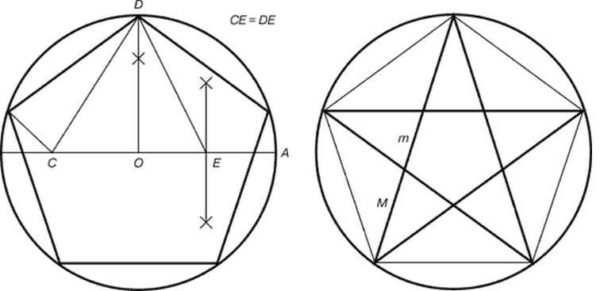
- Pusat bulatan dilambangkan dengan O, lukis garis lurus melaluinya sehingga bersilang dengan bulatan. Salah satu titik persimpangan dilambangkan A... Segmen garis OA Adakah diameter bulatan.
- Cari bahagian tengah segmen OD, meletakkan titik E... Kembalikan tegak lurus dari pusat bulatan hingga ke persimpangan dengan bulatan. Inilah maksudnya D.
- Sambungkan titik E dan D... Dengan bantuan kompas, kami menangguhkan titik pada jari-jari C... Segmen garis CD sama dengan panjang segmen ED... Kami mengukur panjang segmen dengan kompasED... Kami meletakkan jarum ke titik E, arahkan plumbum ke persimpangan dengan jejari. Oleh itu, kita dapat maksudnya C.
- Panjang segmen DC - sisi pentagram. Kami mengukurnya, dengan bantuan kompas kami memindahkannya ke bulatan. Untuk melakukan ini, dengan kompas dengan jarak yang tertunda, kami meletakkan empat titik lagi pada bulatan, menghubungkannya secara bergiliran, kami mendapat pentagram.
Inilah yang menarik, jika bucu pentagram yang dihasilkan digunakan untuk menarik bintang, ia akan terdiri daripada segitiga sempurna.
Permohonan dalam pembinaan
Seperti yang telah disebutkan, tidak diketahui siapa yang menemukan nisbah keemasan, tetapi semua yang kelihatan cantik bagi kita mempunyai nisbah aspek ini. Terdapat banyak contoh di alam. Sekiranya kita mempertimbangkan bangunan terkenal, maka ada juga corak yang sama.
Sekiranya anda mahukan rumah anda di dalam dan luar menjadi menarik, diingati dan disukai, sekurang-kurangnya perkadaran asas dapat dikira semasa membuat atau memilih projek. Mungkin tidak mudah membuat penyesuaian berkadar dan sering melibatkan kos tambahan. Tetapi, jika, semasa membuat projek, anda segera ingat nisbah keemasan, soalan itu sendiri hilang. Sebenarnya tidak begitu sukar.
Sebagai contoh, anggap anda mahukan kediaman seluas 100 meter persegi. Bahagian panjangnya boleh ditarik hingga 12 meter. Maka yang pendek itu panjangnya 62% dan berukuran 7.44 meter. Anda boleh membuat 7 meter atau 7.5, anda boleh meningkatkannya menjadi 8. Tepat, hingga satu sentimeter, pematuhan terhadap dimensi sama sekali tidak diperlukan. Nisbah itu penting. Dan "dengan mata" walaupun dalam pendekatan kelihatan harmoni. Kawasan bangunan dalam kes ini sedikit lebih kecil - 90-96 kotak. Sekiranya anda memerlukan lebih banyak, ambil sisi panjang sama dengan 13 meter dan hitung semula. Nampaknya bagaimana menggunakan nisbah keemasan ketika membuat rancangan rumah dapat difahami.

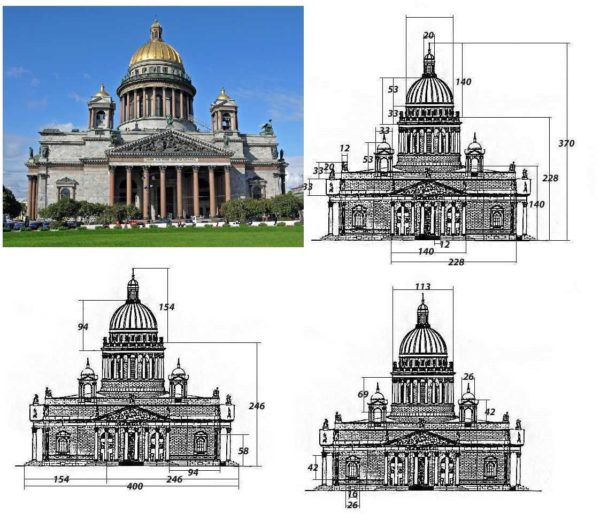
Sekiranya parameter utama bangunan berada dalam perkadaran yang betul, bangunan itu kelihatan menarik dengan gaya apa pun.
Ketinggian lantai dalam kes ini diambil sebagai 32% bahagian terpanjang. Ia akan berukuran 12 * 0.32 = 3.84 meter. Pada prinsipnya, ini sesuai dengan idea semasa mengenai dimensi bilik yang selesa, tetapi jika anda mahu, ketinggian anda dapat lebih kecil. Semua serpihan rumah yang lain juga dikira kira-kira.
Jangan lupa bahawa rumah itu juga mesti sesuai dengan pemandangan. Sekiranya terdapat semacam dominan - bukit tinggi, misalnya, maka perlu untuk menghitung nisbah dengan bukit dan dengan bahagian plot. Secara amnya, untuk mewujudkan harta tanah yang harmoni, banyak faktor mesti diambil kira.

Bukan hanya garis lurus yang boleh digunakan. Benar, lebih sukar untuk bekerja dengan permukaan melengkung, dan harganya lebih mahal - peranti bukan standard selalu lebih mahal
Menurut prinsip yang sama, mereka mengembangkan susun atur dalaman, berusaha, jika mungkin, untuk mematuhi nisbah yang diperlukan. Tetapi kami akan mengulangi sekali lagi: jika boleh. Jangan tergantung pada korespondensi tepat dengan sentimeter. Trend umum adalah penting.
Nisbah emas dalam reka bentuk dalaman
Apa lagi yang disediakan oleh Golden Ratio selain kenikmatan visual? Ahli psikologi mengatakan bahawa seseorang merasa lebih selesa di kawasan dalaman yang dibuat mengikut peraturan ini. Ini tentu saja subjektif, tetapi anda boleh mencuba. Jadi, inilah cara nisbah emas ditafsirkan dalam reka bentuk dalaman:
- Sekiranya anda akan membahagikan ruangan menjadi zon, gunakan peraturan. Ini bermaksud bahawa salah satu bahagiannya mestilah sekitar 62%, yang lain - 38%.
- Kawasan yang diduduki oleh perabot tidak boleh lebih dari 2/3.
- Semasa memilih perabot, kami dipandu oleh peraturan: setiap item bersaiz sederhana tergolong dalam barang besar dengan cara yang sama seperti barang kecil hingga sederhana.
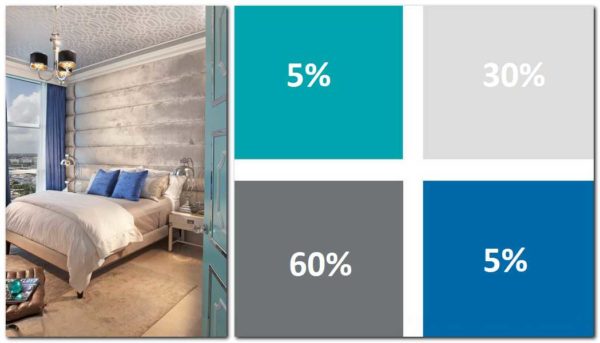
- Semasa memilih warna, ikuti peraturan yang hampir sama:
- Warna utama kira-kira 2/3, semua warna tambahan dan aksen adalah 1/3. Warna dipilih untuk dipadankan mengikut peraturan tertentu.
- Pilihan kedua: 60% adalah warna utama, 30% adalah tambahan dan 10% adalah aksen.
- Apabila menggunakan pembahagian dinding mendatar (panel), ketinggian panel dapat diambil sebagai 1/3 atau 2/3 dari jumlah ketinggian ruangan. Tetapi pada masa yang sama, perabot dipilih berkadar tinggi, dan tidak panjang.
Mengenai perabot, peraturan itu sepertinya tidak dapat difahami, tetapi ini hanya pada pandangan pertama. Sebagai contoh, kami memilih kumpulan rekreasi. Objek besar dalam kes ini adalah sofa atau sofa. Medium - meja kopi atau kopi, kerusi berlengan. Yang kecil - aksesori. Jadi, dimensi meja kopi tidak boleh lebih dari sisi sofa yang panjang, kerusi berlengan - tidak lebih dari sisi pendeknya. Aksesori tidak lebih besar daripada meja atau kerusi. Sebaik-baiknya, mereka berkorelasi dengan mereka sebagai 62% dan 38%.
Mengapa nisbah tepat tidak ditunjukkan? Kerana, pertama, mencari barang seperti itu tidak realistik. Kedua, nisbah emas bukan hanya 62% dan 38%. Ini juga merupakan urutan Fibonacci, yang juga menjadikan reka bentuknya harmoni. Ada orang yang mempunyai urutan ini sebagai "fungsi terbina dalam". Mereka tidak perlu mengira, mereka memilih berdasarkan bakat dan gerak hati. Tetapi jika anda menganalisis pilihan mereka, perkadaran akan hampir ideal. Seperti ini.
Nisbah emas dalam reka bentuk landskap
Semasa membuat lanskap di laman web, prinsip perkadaran ideal diterapkan, menyebutnya sebagai peraturan segitiga. Komposisi harus mempunyai satu yang dominan, selebihnya komponennya hanya menekankan, membayanginya. Contohnya, terdapat sebatang pokok besar di kawasan lot dan anda mahu menewaskannya. Ia akan menjadi pusat komposisi - yang dominan. Letakkannya pada rancangan, susun katil bunga atau rockery, rock garden - perkara yang anda mahu lakukan.
Dari tumbuhan atau batu yang dominan, lukis dua garis pada sudut tepat. Tanaman yang lebih rendah perlu ditanam di garisan ini. Lebih-lebih lagi, tertinggi kedua tidak boleh lebih tinggi daripada 2/3 ketinggian objek utama. Objek ketiga tidak lebih tinggi daripada 1/3. Mereka melengkapkan komposisi dengan penanaman yang lebih banyak. Ini adalah panduan ringkas bagaimana menerapkan nisbah keemasan dalam perancangan penanaman.
Tetapi bukan itu sahaja. Tumbuhan mesti dipilih mengikut warna - gabungan kehijauan dengan pelbagai warna, bintik-bintik bunga dan tumbuh-tumbuhan dekuratif - semuanya mematuhi undang-undang yang sama. Warna yang dominan adalah sekitar 60%, warna pelengkap - 30%, aksen - 10%. Ini jika kita membincangkan peraturan pemilihan dalam satu kumpulan. Tetapi perlu juga untuk menyelaraskan keseluruhan rancangan secara keseluruhan - dalam ukuran, tinggi, warna.