Zelta koeficienta likums arhitektūrā, būvniecībā un dizainā

Dabas novērojumi un mēģinājumi atklāt viņas skaisto radību noslēpumus ir nesuši daudz atklājumu. Viens no tiem ir zelta attiecība. Tas ir noteikts modelis, kas pakļaujas visam, ko mēs saucam par skaistu. Cilvēki, dzīvnieki, ziedi, ēkas, galaktikas ...

Kas ir zelta attiecība un kā to saprast

Bieži sastopamies ar mājām, priekšmetiem, ēkām, augiem, kas mūs kaut ko aizrauj. Cilvēki jau sen ir mēģinājuši saprast, kāpēc viena lieta mums šķiet skaista, otra ne, viņi meklēja modeļus. Un šķiet, ka viņi to ir atraduši. Šī ir noteikta daļu attiecība, ko sauca par zelta attiecību.

Par to, kurš un kad izgudroja zelta koeficientu, neviens precīzi nezina. Kāds šo atklājumu piedēvē Pitagoram, taču pirmais pieminējums tika atrasts Eiklida “Elementos”, un viņš dzīvoja 3. gadsimtā pirms mūsu ēras. Tātad atradums ir acīmredzami vecs. Pēc šī principa tika uzcelti sengrieķu un romiešu tempļi. Protams, tās var būt sakritības, taču tās ir ļoti dīvainas un to ir ļoti daudz. Tātad, visticamāk, viņi apzinājās ideālās proporcijas.

Uz pārdzīvojušajām senatnes ēkām attiecas arī zelta sadaļas likums

Ir pilnīgi skaidrs, ka Leonardo da Vinči meklēja apstiprinājumu šim principam cilvēka ķermeņa struktūrā. Un, kas ir visinteresantākais, es to atradu. Tām sejām un ķermeņiem, kas mums šķiet skaisti, ir proporcijas, kas tikai pakļaujas zelta proporcijas likumam.

Formālā definīcija izklausās gan vienkārši, gan sarežģīti. Tas ir saistīts ar diviem dažāda lieluma segmentiem. Šis princips izklausās apmēram šādi: ja segments ir sadalīts divās nevienādās daļās, tad šis sadalījums būs proporcionāls, ja lielākā daļa segmenta attiecas uz kopumu tāpat kā mazākā daļa uz lielāko. Tas būs skaidrāk, ja paskatīsities uz ilustrāciju un formulu.

Zelta koeficienta princips un formula

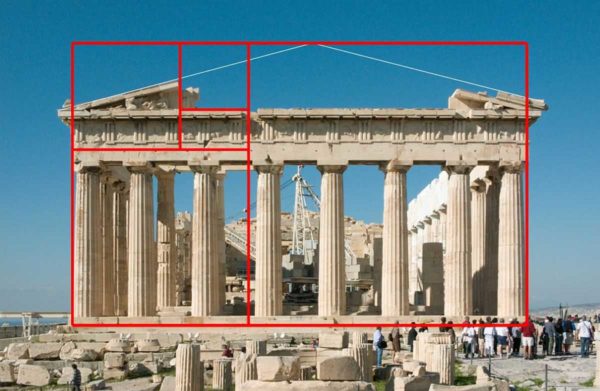
Attēlā viss segments ir sadalīts tā, ka, ja a sadalīt b, mēs iegūstam 1,1618, to pašu skaitli iegūst, ja visu segmentu sadala ar lielu daļu - a... Šis skaitlis ir ideālās proporcijas iemiesojums. Tagad, ja paskatās uz Partenona attēlu, šīs struktūras proporcijas arī ievēro norādīto attiecību.

To pašu modeli var attēlot kā procentus. Varbūt kādam ir vieglāk. Lai veseluma sadalījums būtu proporcionāls, daļām jābūt 62% un 38%. Šādi atcerēties varētu būt vieglāk.

Fibonači secība nav tikai matemātiska formula

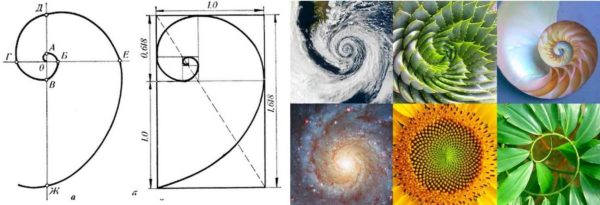
Šo modeli tālāk izstrādāja matemātiķis Fibonači. Viņš izstrādāja skaitlisku secību, kuras elementi, sākot no devītā, ievēro to pašu likumu. Šīs secības grafiskais attēlojums ir spirāle. Ja paskatās uzmanīgi, dabā, arhitektūrā un cilvēka ķermenī ir skaistuma proporcijas.

Kā veidot taisnstūri ar perfektām proporcijām

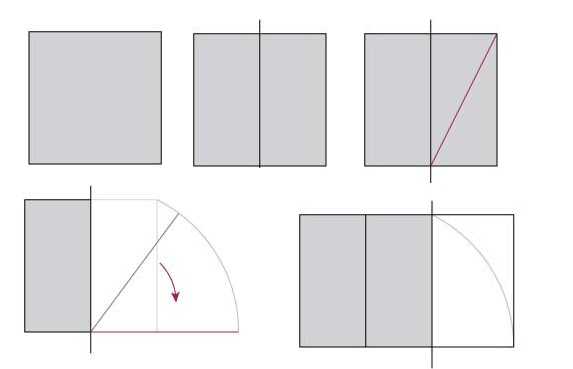
Lai saņemto informāciju varētu pielietot praksē, kaut kā jāiemācās sadalīt telpu vai veidot to saskaņā ar šo likumu. Pirmkārt, iemācīsimies veidot taisnstūri ar perfektām proporcijām. Par pamatu ņemam kvadrātu.

Izveido taisnstūri ar zelta attiecību

Sadaliet kvadrātu uz pusēm, vienā no iegūtajiem taisnstūriem uzzīmējiet līniju, kas savieno pretējos stūrus. Tad mēs ņemam kompasu, ielieciet adatu kvadrāta apakšējās malas centrā, atstājiet iegūtās diagonāles garumu un atzīmējiet to uz līnijas, kas būs kvadrāta apakšējās puses turpinājums.Iegūtā taisnstūra malu attiecība ir 1,62 (tieši šī attiecība dod 62% un 38%).

Tas acīmredzami nav nejaušība. Lai gan ne viss pakļaujas šim paraugam

Kas ir interesantāk, ka, ja jūs sākat sadalīt 1,62 taisnstūri kvadrātā un taisnstūrī, jūs atkal iegūsiet taisnstūri ar perfektām proporcijām, bet mazāku. Ja jūs to atkal sadalīsit pēc tā paša principa, būs vēl viens kvadrātveida + taisnstūra pāris ar malām, kuru attiecība atbildīs zelta proporcijai. Un tā tālāk, līdz jūs varat veikt sadalīšanu. Bet kas ir vēl interesantāk, Fibonacci sērija lieliski iekļaujas šajā sadalījumā, kas izskatās kā atritinoša spirāle. Skatīt ilustrāciju attēlā iepriekš.

Kā sadalīt segmentu saskaņā ar zelta koeficienta likumu

Šī prasme noderēs, piemēram, veidojot mājas projektu, plānojot, izstrādājot dzīvokļa dizainu, sakārtojot mēbeles utt. Tas var būt vajadzīgs arī, plānojot vietu, puķu dobes, stādot augus utt. Kopumā to var izmantot gandrīz visur.

Nekas nav iedomāts, bet jūs nevarat novērst acis. Vai Tu zini kapēc?

Tātad, segmenta sadalīšanas secība saskaņā ar zelta sadaļas likumu:

• Mēs ņemam segmentu, sadalām to uz pusēm.
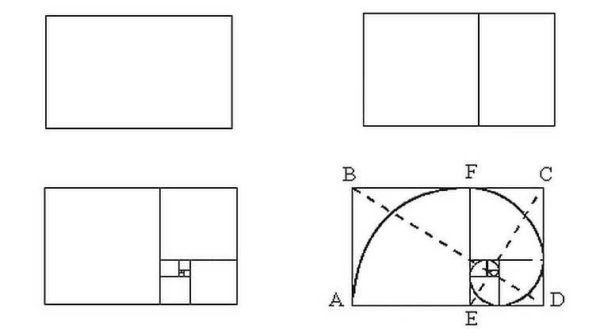
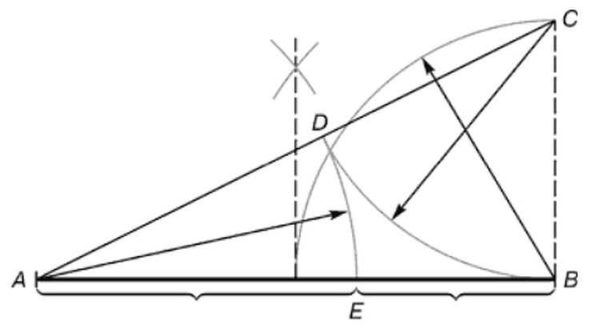
• No viena no galiem mēs atjaunojam perpendikulu (taisna līnija 90 ° leņķī), kas ir puse no segmenta garuma. Attēlā tas ir segments BC.
• Saņemtais punkts C savienojiet taisnu līniju ar segmenta otru galu (A).
• Par segmentu AC pieliek punktu D... Tas atrodas attālumā, kas vienāds ar segmenta garumu BC... Vieglākais veids, kā to izdarīt, ir kompass, taču varat izmantot arī lineālu.
• Mēs izmērām segmenta garumu AD (atkal ar kompasu vai lineālu). Mēs atliekam to pašu garumu uz segmentu AB... Mēs saprotam punktu E.
• Tagad, ja jūs izmērīsit segmentu garumus AE un EB un sadaliet tos, iegūstam to pašu kāroto skaitli - 1,62.

Segmenta sadalīšana sekcijās ar ideālu attiecību

Pāris reizes atkārtojot procedūru, jūs uzzināsiet, kā visu izdarīt burtiski dažu minūšu laikā. Ja jums, piemēram, nepieciešams noteikt loga augstumu, tā formu, varat izmantot arī šīs proporcijas. Pēc tā paša principa ir iespējams noteikt visu arhitektūras elementu atrašanās vietu, to izmērus. Plānojot esošos objektus, to ir vieglāk sadalīt, izmantojot procentus. Šeit jūs vai nu skaitāt galvā, vai arī izmantojat kalkulatoru.

Ideāls trīsstūris un pentagramma

Par ideālu tiek dēvēts vienādsānu trijstūris, kura pamatne norāda uz sānu garumu kā 1/3. Tas ir, atkal tiek novērota zelta attiecība. Trīsstūra zīmēšana ar ideālu malu attiecību nav grūta. Tas ir ērtāk ar kompasu, bet jūs varat iztikt ar lineālu.

Zelta trīsstūris, noteikums par tā uzbūvi un piemērošanu, piemēram, interjera veidošanā

Konstrukcija ir šāda. Taisnā līnijā no punkta A trīs reizes atlikt patvaļīga garuma segmentu. Mēs apzīmējam šo garumu O... Mēs saprotam punktu B... Caur to velciet taisnu līniju perpendikulāri segmentam AB... Šajā līnijā uz abām punkta pusēm B atlikt vērtību O... Mēs iegūstam divus punktus d un d1... Mēs tos savienojam ar punktu A... Tātad mēs saņēmām trīsstūri, kura malas ir saistītas kā 1,62. To var pārbaudīt, ja atlikt pamatnes garumu sānos ar kompasu (punkts C). Otra pārbaude ir tāda, ka pretējais leņķis ir 36 °.

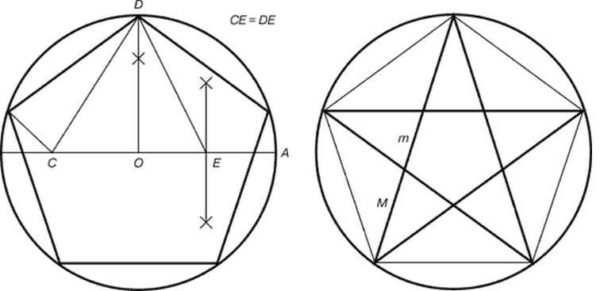
Pentagrammas veidošana ir nedaudz sarežģītāka. Mēs to ierakstām lokā, mēs nevaram iztikt bez kompasa.

• Apļa centru apzīmē ar O, caur to velciet taisnu līniju, līdz tā krustojas ar apli. Viens no krustošanās punktiem ir apzīmēts A... Līnijas segments OA Vai apļa diametrs.
• Atrodiet segmenta vidu OD, ielieciet punktu E... Atjaunojiet perpendikulu no apļa centra līdz krustojumam ar apli. Šis ir punkts D.

Pentagrammas veidošana

• Savienojiet punktus E un D... Ar kompasa palīdzību mēs atliekam punktu rādiusā C... Līnijas segments CD vienāds ar segmenta garumu ED... Mēs izmērām segmenta garumu ar kompasuED... Mēs pieliekam adatu līdz punktam E, vediet vadu uz krustojumu ar rādiusu. Tātad mēs sapratām punktu C.
• Segmenta garums DC - pentagramas puse. Mēs to izmērām, ar kompasa palīdzību mēs to pārvietojam uz apli. Lai to izdarītu, ar kompasu ar novēlotu attālumu mēs uzliekam vēl četrus punktus uz apļa, savienojot tos pēc kārtas, mēs iegūstam pentagrammu.

Lūk, kas ir interesants, ja iegūtās pentagrammas virsotnes izmanto, lai uzzīmētu zvaigzni, tā sastāvēs no perfektiem trīsstūriem.

Pielietojums būvniecībā

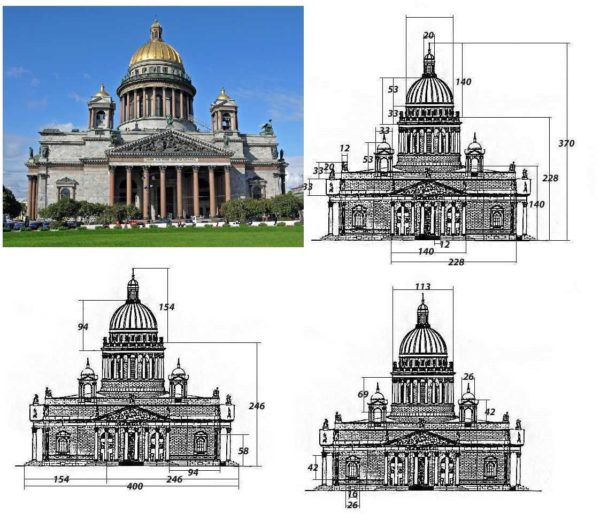
Kā jau minēts, nav zināms, kurš atklāja zelta proporciju, taču visam, kas mums šķiet skaists, ir tieši šāda proporcija. Dabā ir daudz piemēru. Ja mēs ņemam vērā labi zināmas ēkas, tad ir arī tas pats modelis.

Īzaka katedrāle - jūs varat rēķināties prieka pēc

Ja vēlaties, lai jūsu mājas iekšpusē un ārpusē būtu pievilcīgas, atceras un iepatiktos, izveidojot vai izvēloties projektu, var aprēķināt vismaz pamata proporcijas. Iespējams, ka ne vienmēr ir viegli veikt proporcionālas korekcijas un tas bieži vien rada papildu izmaksas. Bet, ja, veidojot projektu, jūs nekavējoties paturat prātā zelta koeficientu, paši jautājumi pazūd. Tas patiesībā nav tik grūti.

Piemēram, pieņemsim, ka vēlaties māju apmēram 100 kvadrātmetru platībā. Garajā pusē var veikt līdz 12 metriem. Tad īsais ir 62% no garā un būs 7,44 metri. Jūs varat veikt 7 metrus vai 7,5 metrus, jūs varat palielināt to līdz 8. Precīzi, līdz centimetram, izmēru ievērošana nemaz nav nepieciešama. Attiecība ir svarīga. Un "no acīm" pat pieeja izskatās harmoniski. Apbūves laukums šajā gadījumā ir nedaudz mazāks - 90-96 kvadrāti. Ja jums vajag vairāk, paņemiet garo malu, kas vienāds ar 13 metriem, un skaitiet vēlreiz. Šķiet, ka ir saprotams, kā izmantot zelta attiecību, veidojot mājas plānu.

Ja galvenie ēkas parametri ir pareizā proporcijā, ēka izskatās interesanta jebkurā stilā.

Grīdas augstums šajā gadījumā tiek ņemts par 32% no garākās daļas. Tas būs 12 * 0,32 = 3,84 metri. Principā tas atbilst pašreizējām idejām par telpas ērtajiem izmēriem, bet, ja vēlaties, varat padarīt augstumu mazāku. Aptuveni tiek aprēķināti arī visi pārējie mājas fragmenti.

Neaizmirstiet, ka mājai jāiekļaujas arī ainavā. Ja ir kāda veida dominējošā - piemēram, augsts kalns, tad jāaprēķina attiecība ar kalnu un ar zemes gabala proporcijām. Kopumā, lai izveidotu harmonisku īpašumu, jāņem vērā daudzi faktori.

Var izmantot ne tikai taisnas līnijas. Tiesa, strādāt ar izliektām virsmām ir grūtāk, un tās maksā vairāk - nestandarta ierīce vienmēr ir dārgāka

Saskaņā ar to pašu principu viņi izstrādā iekšējo izkārtojumu, cenšoties, ja iespējams, ievērot nepieciešamo attiecību. Bet mēs vēlreiz atkārtosim: ja iespējams. Nepieķerieties ar precīzu atbilstību centimetram. Svarīga ir vispārējā tendence.

Zelta attiecība interjera dizainā

Ko vēl Zelta attiecība sniedz bez vizuāla baudījuma? Psihologi saka, ka interjerā, kas izveidots saskaņā ar šo noteikumu, cilvēks jūtas ērtāk. Tas, protams, ir subjektīvs, bet jūs varat mēģināt. Tātad, interjera dizainā tiek interpretēta zelta attiecība:

• Ja jūs plānojat sadalīt telpu zonās, izmantojiet noteikumu. Tas nozīmē, ka vienai no daļām jābūt aptuveni 62%, otrai - 38%.
• Mēbeļu gabaliem paredzētajai platībai nevajadzētu būt lielākai par 2/3.
• Izvēloties mēbeles, mēs vadāmies pēc noteikuma: katrs vidējais priekšmets izmēru ziņā attiecas gan uz lieliem, gan uz maziem un vidējiem.
• Izvēloties krāsu, ievērojiet aptuveni tos pašus noteikumus:
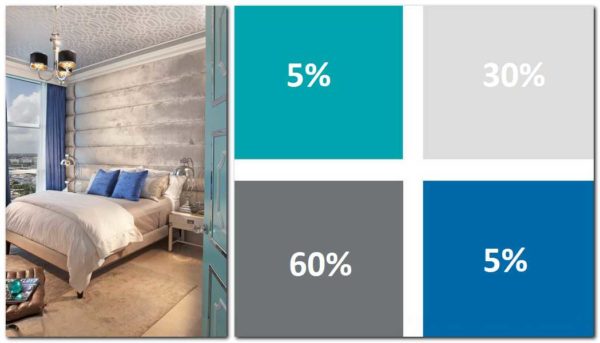
  • Galvenā krāsa ir aptuveni 2/3, visas papildu un akcentu krāsas ir 1/3. Krāsas tiek izvēlētas atbilstoši noteiktiem noteikumiem.
  • Otrais variants: 60% ir galvenā krāsa, 30% ir papildu un 10% ir akcents.
    

    Krāsu saskaņošanas piemērs atbilstoši pareizas proporcionalitātes noteikumiem

• Izmantojot sienas (paneļa) horizontālo sadalījumu, paneļa augstumu var uzskatīt par 1/3 vai 2/3 no kopējā telpas augstuma. Bet tajā pašā laikā mēbeles tiek izvēlētas proporcionāli augstumam, nevis garumam.

Attiecībā uz mēbelēm likums šķiet nesaprotams, taču tas ir tikai no pirmā acu uzmetiena. Piemēram, mēs izvēlamies atpūtas grupu. Liels objekts šajā gadījumā ir dīvāns vai dīvāns. Vidējs - kafijas vai kafijas galdiņš, atzveltnes krēsli. Mazie - aksesuāri. Tātad, kafijas galdiņa izmēri nedrīkst būt vairāk kā dīvāna garā puse, atzveltnes krēsls - ne vairāk kā tā īsā puse. Piederumi nav lielāki par galdu vai krēsliem. Ideālā gadījumā tie korelē ar viņiem kā 62% un 38%.

Proporcionalitāte ir svarīga lieta

Kāpēc nav norādīta precīza attiecība? Jo, pirmkārt, šādu priekšmetu atrašana ir nereāla. Otrkārt, zelta attiecība ir ne tikai 62% un 38%. Tā ir arī Fibonači secība, kas arī padara dizainu harmonisku. Ir cilvēki, kuriem šī secība ir "iebūvēta funkcija". Viņiem nav nepieciešams skaitīt, viņi izvēlas, pamatojoties uz nojauta un intuīciju. Bet, ja analizējat viņu izvēli, proporcijas būs tuvu ideālajām. Kā šis.

Zelta attiecība ainavu dizains

Veidojot ainavu vietnē, tiek piemērots ideālo proporciju princips, to nosaucot par trīsstūra likumu. Kompozīcijai vajadzētu būt vienam dominējošam, pārējie komponenti to tikai uzsver, ieskaita. Piemēram, uz zemes gabala ir liels koks, kuru vēlaties pārspēt. Tas būs skaņdarba centrs - dominējošais. Ievietojiet to plānā, sakārtojiet to rindā ziedu gulta vai rockery, akmens dārzs - tas, ko vēlaties darīt.

Trijstūra likums dārza dizainā

No dominējošā auga vai akmens izvelciet divas līnijas taisnā leņķī. Uz šīm līnijām būs jāstāda zemāki augi. Turklāt otrais augstākais nedrīkst būt augstāks par 2/3 no galvenā objekta augstuma. Trešais objekts nav augstāks par 1/3. Viņi papildina kompozīciju ar vēl vairāk apstulbinātiem stādījumiem. Šis ir īss ceļvedis, kā piemērot zelta attiecību stādīšanas plānošanā.

Bet tas vēl nav viss. Augi jāizvēlas pēc krāsas - dažādu toņu apstādījumu, ziedu plankumu un dekoratīvo lapu augu kombinācija - viss pakļaujas vienam likumam. Dominējošais tonis ir aptuveni 60%, papildkrāsas - 30%, akcenti - 10%. Tas ir, ja mēs runājam par atlases noteikumiem vienā grupā. Bet jāsaskaņo arī viss plāns kopumā - izmēros, augstumā, krāsās.