La regla de la proporció àuria en arquitectura, construcció i disseny
Les observacions de la natura i els intents de descobrir els secrets de les seves belles criatures han portat molts descobriments. Un d’ells és la proporció àuria. Aquest és un patró determinat que obeeix a tot allò que anomenem bell. Persones, animals, flors, edificis, galàxies ...
El contingut de l'article
- 1 Quina és la proporció àuria i com entendre-la
- 2 Com es construeix un rectangle amb proporcions perfectes
- 3 Com es divideix un segment segons la regla de la proporció àuria
- 4 Triangle i pentagrama perfectes
- 5 Aplicació en construcció
- 6 Relació àuria en interiorisme
- 7 La proporció àuria en el disseny de paisatges
Quina és la proporció àuria i com entendre-la
Sovint ens trobem amb cases, objectes, edificis, plantes que ens fascinen amb alguna cosa. La gent fa temps que intenta entendre per què una cosa ens sembla bella, l’altra no, buscava patrons. I sembla que l’han trobat. Es tracta d’una certa proporció de parts, que es deia la proporció àuria.
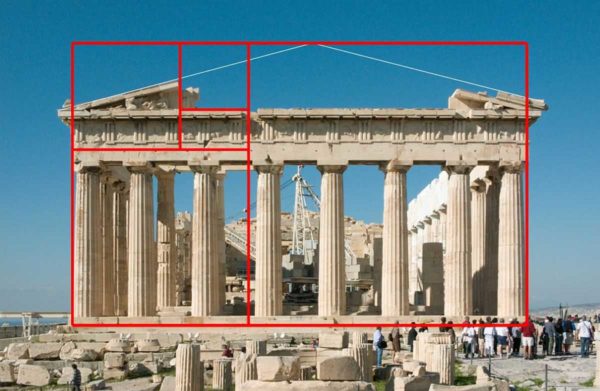
Ningú no sap exactament qui i quan va inventar la proporció àurea. Algú atribueix el descobriment a Pitàgores, però la primera menció es va trobar als "Elements" d'Euclides i va viure al segle III aC. Per tant, la troballa és clarament antiga. És amb aquest principi que es van construir antics temples grecs i romans. Per descomptat, poden ser coincidències, però són molt estranyes i n’hi ha moltes. De manera que, molt probablement, eren conscients de les proporcions ideals.
És absolutament segur que Leonardo da Vinci buscava la confirmació d’aquest principi en l’estructura del cos humà. I, el que és més interessant, ho vaig trobar. Aquelles cares i cossos que ens semblen bells tenen proporcions que només compleixen la llei de la proporció àuria.
La definició formal sona simple i complexa. S'associa amb dos segments de mides diferents. Aquest principi sona així: si un segment es divideix en dues parts desiguals, llavors aquesta divisió serà proporcional si la majoria del segment fa referència al conjunt de la mateixa manera que la part més petita a la més gran. Serà més clar si mireu la il·lustració i la fórmula.
A la figura, es divideix tot el segment de manera que si a dividit en b, obtenim 1,1618, la mateixa xifra s’obté si tot el segment es divideix per una gran part - a... Aquest nombre és l’encarnació de la proporció ideal. Ara, si mireu la imatge del Partenó, les proporcions d’aquesta estructura també obeeixen la proporció indicada.
Es pot representar el mateix patró com a percentatges. Potser és més fàcil per a algú. Per tal que la divisió del conjunt sigui proporcional, les parts han de ser del 62% i del 38%. Pot ser que sigui més fàcil recordar-ho d’aquesta manera.
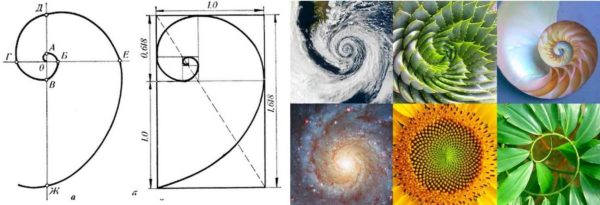
Aquest patró va ser desenvolupat encara més pel matemàtic Fibonacci. Va desenvolupar una seqüència numèrica, els elements de la qual, a partir de la novena, obeeixen la mateixa llei. La representació gràfica d’aquesta seqüència és una espiral. Si us fixeu bé, hi ha proporcions de bellesa a la natura, a l’arquitectura i al cos humà.
Com es construeix un rectangle amb proporcions perfectes
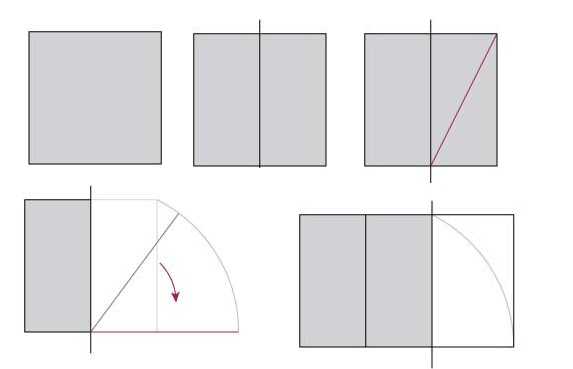
Per aplicar la informació rebuda a la pràctica, d'alguna manera s'ha d'aprendre a dividir l'espai o construir-lo d'acord amb aquesta llei. En primer lloc, aprenem a construir un rectangle amb proporcions perfectes. Prenem com a base un quadrat.
Divideix el quadrat per la meitat, dibuixa una línia en un dels rectangles resultants que connecti les cantonades oposades. Després agafem una brúixola, posem l’agulla al centre del costat inferior del quadrat, reservem la longitud de la diagonal resultant i la marquem en una línia que serà la continuació del costat inferior del quadrat.El rectangle resultant té una relació d'aspecte d'1,62 (és exactament la proporció que dóna el 62% i el 38%).
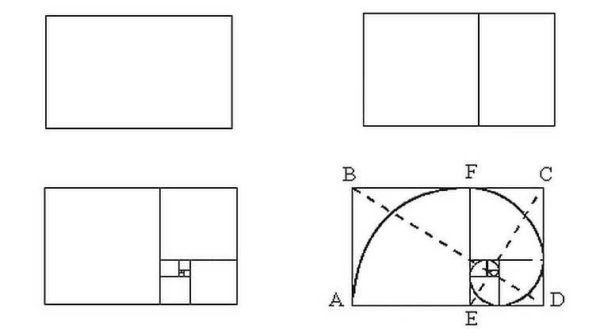
El més interessant és que si comenceu a dividir el rectangle 1,62 en un quadrat i un rectangle, obtindreu de nou un rectangle amb proporcions perfectes, però més petit. Si el torneu a dividir segons el mateix principi, hi haurà un altre parell de quadrat + rectangle amb costats, la proporció dels quals correspondrà a la proporció àuria. I així successivament fins que pugueu dur a terme la divisió. Però el que és encara més interessant és que la sèrie de Fibonacci s’adapta perfectament a aquesta divisió, que sembla una espiral desenfadada. Veure la il·lustració a la imatge superior.
Com es divideix un segment segons la regla de la proporció àuria
Aquesta habilitat serà útil, per exemple, a l’hora de crear un projecte de casa, planificar, dissenyar un apartament, organitzar mobles, etc. També pot ser necessari quan planifiqueu un lloc, parterres de flors, plantar plantes, etc. En general, es pot utilitzar gairebé a tot arreu.
Per tant, l’ordre de dividir un segment segons la regla de la secció daurada:
- Agafem un segment, el dividim per la meitat.
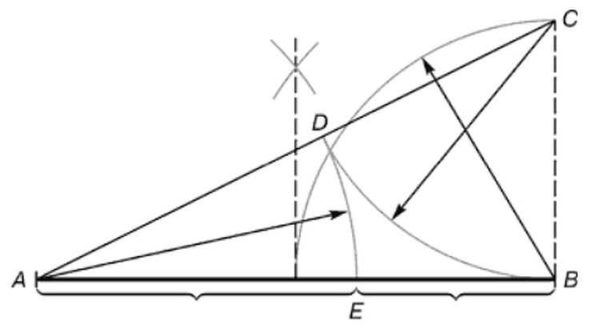
- Des d’un dels extrems restaurem una perpendicular (línia recta amb un angle de 90 °), que és la meitat de la longitud del segment. A la figura, es tracta d’un segment AC.
- Punt rebut C connectar una línia recta amb l'altre extrem del segment (A).
- Al segment AC posar un punt D... Es troba a una distància igual a la longitud del segment AC... La manera més senzilla de fer-ho és amb una brúixola, però també podeu utilitzar una regla.
- Mesurem la longitud del segment AD (de nou amb una brúixola o un regle). Ajornem la mateixa longitud al segment AB... Tenim el punt E.
- Ara, si mesureu les longituds dels segments AE i EB i dividim-los, obtenim el mateix número desitjat: 1,62.
Repetint el procediment un parell de vegades, aprendràs a fer-ho tot literalment en qüestió de minuts. Si necessiteu, per exemple, determinar l’alçada de la finestra, la seva forma, també podeu utilitzar aquestes proporcions. Pel mateix principi, és possible determinar la ubicació de tots els elements arquitectònics, les seves mides. Quan planifiqueu objectes existents, és més fàcil dividir-lo mitjançant un percentatge. Aquí podeu comptar al cap o utilitzar una calculadora.
Triangle i pentagrama perfectes
Un triangle isòsceles s’anomena ideal, la base del qual es refereix a la longitud del costat com a 1/3. És a dir, de nou s’observa la proporció àuria. És fàcil dibuixar un triangle amb la relació d’aspecte perfecta. És més convenient amb una brúixola, però es pot aconseguir amb una regla.

El triangle daurat, la regla de la seva construcció i aplicació en la creació d’un interior, per exemple
La construcció és la següent. En línia recta des d’un punt A ajornar tres vegades un segment de longitud arbitrària. Denotem aquesta longitud O... Tenim el punt B... Dibuixeu una línia recta a través d’ella, perpendicular al segment AB... En aquesta línia cap als dos costats del punt B reserveu el valor O... Obtenim dos punts d i d1... Els connectem amb un punt A... Així doncs, vam obtenir un triangle, els costats del qual estan relacionats com a 1,62. Podeu comprovar-ho si posposeu la longitud de la base del costat lateral amb una brúixola (punt C). La segona comprovació és que l’angle oposat és de 36 °.
Construir un pentagrama és una mica més complicat. L’inscrivim en un cercle, no podem prescindir d’una brúixola.
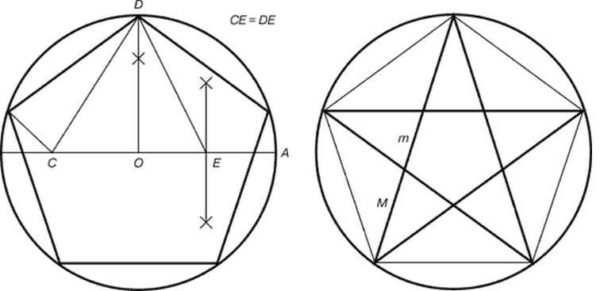
- El centre del cercle es denota amb O, traça una línia recta a través d’ella fins que es creui amb el cercle. Es denota un dels punts d’intersecció A... Segment de línia OA És el diàmetre del cercle.
- Cerqueu la meitat del segment OD, posa un punt E... Restaura la perpendicular des del centre del cercle fins a la intersecció amb el cercle. Aquest és el punt D.
- Connecteu els punts E i D... Amb l’ajut d’una brúixola, posposem un punt del radi C... Segment de línia CD igual a la longitud del segment ED... Mesurem la longitud del segment amb una brúixolaED... Posem l’agulla al punt E, conduïu el plom fins a la intersecció amb el radi. Així doncs, vam aconseguir el punt C.
- Longitud del segment DC - el costat del pentagrama. El mesurem, amb l’ajut d’una brúixola el transferim a un cercle. Per fer-ho, amb una brúixola amb una distància retardada, posem quatre punts més al cercle, connectant-los al seu torn, obtenim un pentagrama.
Això és interessant, si els vèrtexs del pentagrama resultant s’utilitzen per dibuixar una estrella, constarà de triangles perfectes.
Aplicació en construcció
Com ja s’ha esmentat, es desconeix qui va descobrir la proporció àuria, però tot el que ens sembla bonic té exactament aquesta relació d’aspecte. Hi ha molts exemples a la natura. Si considerem edificis coneguts, també hi ha el mateix patró.
Si voleu que la vostra llar per dins i per fora sigui atractiva, recordada i agradada, es poden calcular almenys les proporcions bàsiques a l’hora de crear o triar un projecte. Potser no sempre és fàcil fer ajustos proporcionals i sovint comporten costos addicionals. Però, si, en crear un projecte, teniu present immediatament la proporció àurea, les preguntes desapareixen. En realitat no és tan difícil.
Per exemple, suposem que voleu una casa d’uns 100 metres quadrats. El costat llarg es pot agafar fins a 12 metres. Llavors el curt és el 62% del llarg i serà de 7,44 metres. Podeu fer 7 metres o 7,5 metres, podeu augmentar-los a 8. No és del tot necessari el compliment de les dimensions exactes, fins a un centímetre. La relació és important. I "a ull", fins i tot en l'enfocament, sembla harmònic. La superfície edificable en aquest cas és lleugerament més petita: 90-96 quadrats. Si en necessiteu més, agafeu el costat llarg igual a 13 metres i torneu a comptar. Sembla que es pot entendre com utilitzar la proporció àuria a l’hora de crear un pla de casa.

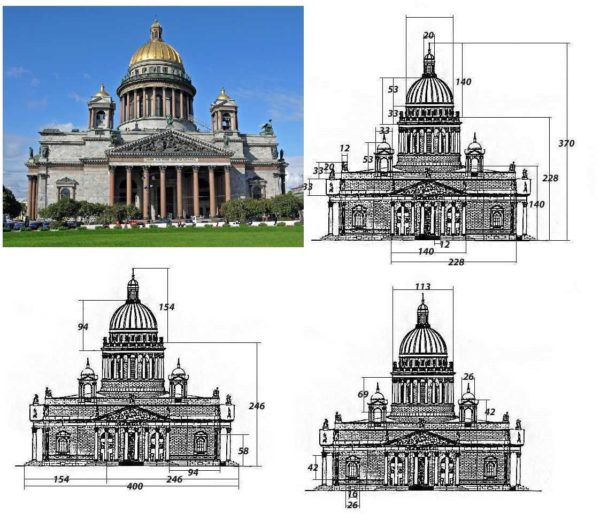
Si els principals paràmetres de l'edifici es troben en la proporció correcta, l'edifici sembla interessant en qualsevol estil.
En aquest cas, l'alçada del sòl es considera el 32% de la part més llarga. Serà 12 * 0,32 = 3,84 metres. En principi, això correspon a les idees actuals sobre les còmodes dimensions de l'habitació, però si ho desitgeu, podeu reduir l'alçada. La resta de fragments de la casa també es calculen aproximadament.
No oblideu que la casa també ha d’adaptar-se al paisatge. Si hi ha algun tipus de dominant: un turó alt, per exemple, s’ha de calcular la relació amb el turó i amb les proporcions de la parcel·la. En general, per crear una propietat harmònica, cal tenir en compte molts factors.

No només es poden utilitzar línies rectes. És cert que és més difícil treballar amb superfícies corbes i costen més: un dispositiu no estàndard sempre és més car
Segons el mateix principi, desenvolupen un disseny intern, intentant, si és possible, complir la proporció requerida. Però repetirem una vegada més: si és possible. No us pengeu de la correspondència exacta amb el centímetre. La tendència general és important.
Relació àuria en interiorisme
Què més proporciona la ràtio d’or a més del gaudi visual? Els psicòlegs diuen que una persona se sent més còmoda en un interior creat segons aquesta regla. Això és, per descomptat, subjectiu, però podeu provar-ho. Per tant, aquí s’explica com interpretar la regla de la proporció àuria en disseny d’interiors:
- Si voleu dividir l'habitació en zones, utilitzeu la regla. Això vol dir que una de les parts hauria de ser aproximadament del 62% i l’altra, del 38%.
- La superfície ocupada pels mobles no pot superar els 2/3.
- A l’hora d’escollir els mobles, ens orientem per la regla: cada article mitjà en termes de dimensions fa referència tant a grans com a petits a mitjans.
- En triar un color, seguiu aproximadament les mateixes regles:
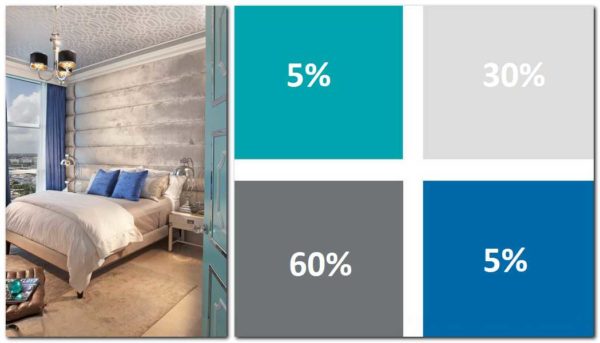
- El color principal és d'aproximadament 2/3, tots els colors addicionals i l'accent són 1/3. Els colors s’escullen segons les regles.
- Segona opció: el 60% és el color principal, el 30% és addicional i el 10% és accent.
- Quan s'utilitza la divisió horitzontal de la paret (tauler), l'alçada del tauler es pot considerar com 1/3 o 2/3 de l'alçada total de la sala. Però, alhora, els mobles es seleccionen proporcionalment en alçada i no en longitud.
Pel que fa als mobles, la norma sembla incomprensible, però això només és a primera vista. Per exemple, seleccionem un grup recreatiu. Un objecte gran en aquest cas és un sofà o un sofà. Mitjana - taula de cafè o cafè, butaques. Petites: accessoris. Per tant, les dimensions de la taula de centre no haurien de ser més que el costat llarg del sofà, la butaca, ni més ni menys que el seu costat curt. Els accessoris no són més grans que una taula o cadires. L’ideal seria que s’hi correlacionessin amb el 62% i el 38%.
Per què no s’indica la proporció exacta? Perquè, en primer lloc, trobar aquests elements no és realista. En segon lloc, la proporció àurea no és només del 62% i del 38%. També és la seqüència de Fibonacci, que segueix, que també fa que el disseny sigui harmònic. Hi ha persones que tenen aquesta seqüència com a "funció integrada". No necessiten comptar, trien en funció del gust i la intuïció. Però si analitzeu la seva elecció, les proporcions seran properes a l’ideal. Com això.
Ràtio àurea en disseny de paisatges
Quan es crea un paisatge en un lloc, s'aplica el principi de proporcions ideals, que s'anomena regla del triangle. La composició hauria de tenir un domini, la resta de components només l’emfatitzen i l’obtenen. Per exemple, hi ha un gran arbre al lot i el voleu guanyar. Serà el centre de la composició: el dominant. Poseu-lo en un pla, feu-lo alinear llit de flors o rocalla, jardí de roques: el que voleu fer.
Des de la planta o la pedra dominant, dibuixeu dues línies en angle recte. En aquestes línies s’hauran de plantar plantes inferiors. A més, el segon màxim no hauria de ser superior a 2/3 de l'alçada de l'objecte principal. El tercer objecte no és superior a 1/3. Complementen la composició amb plantacions encara més retardades. Aquesta és una guia ràpida sobre com aplicar la proporció àuria en la planificació de la plantació.
Però això no és tot. Les plantes s’han de seleccionar pel color (una combinació de vegetació de diferents tons, taques de flors i plantes de fulla caduca decorativa) tot compleix la mateixa llei. La tonalitat dominant és del 60%, els colors complementaris (30%), els accents (10%). Això si parlem de les regles de selecció en un grup. Però també és necessari coordinar tot el pla en conjunt, en mides, alçades i colors.